Η επιλογή της κατάλληλης μεθόδου για τη διδασκαλία της Ευκλείδειας Γεωμετρίας σε παιδιά με Ειδικές Μαθησιακές Δυσκολίες αποτελεί σημαντικό ζήτημα. Στην παρούσα εργασία μελετάμε ορισμένα θεωρητικά θέματα σχετικά με τη διδασκαλία γεωμετρικών εννοιών σε παιδιά με Ειδικές Μαθησιακές Δυσκολίες, εστιάζοντας στο εκπαιδευτικό υλικό. Παρουσιάζουμε τον σχεδιασμό, την υλοποίηση και τα αποτελέσματα μιας ποιοτικής έρευνας που διεξαγάγαμε με έξι μαθητές Γ΄ Γυμνασίου σε ένα Ενιαίο Ειδικό Επαγγελματικό Γυμνάσιο στην Ελλάδα, με θέμα την αξιοποίηση της ιστοσελίδας “Ο Ευκλείδης του Byrne” στη διδασκαλία προτάσεων της Ευκλείδειας Γεωμετρίας. Η έρευνα έδειξε ότι τα παιδιά κατανόησαν τα βασικά σημεία της απόδειξης της πρότασης που τους παρουσιάσαμε και αφομοίωσαν βασικές γεωμετρικές έννοιες και διαδικασίες με τη χρήση των χρωμάτων και των σχημάτων. Η εργασία ολοκληρώνεται με συζήτηση επάνω σε προτάσεις, προοπτικές και περιορισμούς για τη διδασκαλία που αξιοποιεί τον “Ευκλείδη του Byrne”.
Εισαγωγή
Ο όρος “Ειδικές Μαθησιακές Δυσκολίες” (ΕΜΔ) αναφέρεται σε μία ιδιαίτερη κατηγορία δυσκολιών που αφορούν τη μάθηση και κυρίως την κατάκτηση του γραπτού λόγου (Willcutt et al., 2019). Τα Μαθηματικά ως δομή και οι μαθηματικές έννοιες γενικότερα θεωρούνται πολύ σημαντικές τόσο για τη σχολική πορεία του ατόμου με ΕΜΔ, όσο και για την αυτόνομη διαβίωσή του (Barnes et al., 2020). Βασική προϋπόθεση για τη διδασκαλία των Μαθηματικών σε παιδιά με ΕΜΔ αποτελεί η προσαρμογή των υλικών στα ενδιαφέροντά τους και η αξιοποίηση διάφορων εναλλακτικών μέσων, όπως είναι τα οπτικά αντικείμενα, η χρήση χρωμάτων και οι καινοτόμες τεχνολογίες (Jitendra et al., 2018). Σύμφωνα με τη βιβλιογραφία, μία από τις προτεινόμενες στρατηγικές για τη διδασκαλία των Μαθηματικών σε παιδιά με ΕΜΔ είναι η χρήση οπτικών υλικών, εργαλείων και βοηθημάτων, καθώς και η πολυαισθητηριακή μέθοδος κατά την εκπαιδευτική διαδικασία (Marita & Hord, 2017). Έρευνες έχουν επισημάνει τα θετικά μαθησιακά αποτελέσματα της χρήσης οπτικών μεθόδων στη διδασκαλία παιδιών με ΕΜΔ (Grobecker & De Lisi, 2000; Cass et al., 2003).
Στο παρόν άρθρο εστιάζουμε στη διδασκαλία της Γεωμετρίας σε παιδιά με ΕΜΔ, κάνοντας χρήση της καινοτόμου ιστοσελίδας “Ο Ευκλείδης του Byrne”. Ο Άγγλος πολιτικός μηχανικός Oliver Byrne (1810-1880) συνέγραψε, μεταξύ πολλών άλλων ενδιαφερόντων έργων για τα Μαθηματικά και τη Μηχανική, το βιβλίο The first six books of Euclid, το οποίο εκδόθηκε στο Λονδίνο το 1847 (Hawes & Kolpas, 2015). Στο βιβλίο αυτό, αντί για γράμματα και αλγεβρικές σχέσεις για τον προσδιορισμό των γωνιών, των πλευρών και των σχημάτων, χρησιμοποιούνται έγχρωμες αναπαραστάσεις. Πιο συγκεκριμένα, ο Byrne αντικατέστησε τις ακολουθίες ΑΒΓ, ΒΓΑ, ΓΑΒ κ.λπ. με μπλε, κίτρινη και κόκκινη γωνία αντίστοιχα, και με σχεδόν παρόμοιο τρόπο συμβόλισε σημεία, ευθύγραμμα τμήματα, κύκλους, τρίγωνα και αλλά στοιχεία με διαφορετικά είδη χρωμάτων. Με άλλα λόγια, στον “Ευκλείδη του Byrne” ο γραπτός λόγος έχει αντικατασταθεί από χρώματα και σύμβολα. “Ο Ευκλείδης του Byrne” μεταφέρθηκε σε ηλεκτρονική μορφή (βλ. εδώ) το 2018 από τον Nicholas Rougeux, έναν σχεδιαστή ιστοσελίδων, ενώ πολύ γρήγορα μεταφράστηκε στα Ελληνικά και άλλες Ευρωπαϊκές γλώσσες.
Με δεδομένο ότι η Ευκλείδεια Γεωμετρία αποτελεί διαχρονικά βασικό μέρος του Προγράμματος Σπουδών για μαθητές με τυπική και μη τυπική ανάπτυξη στην Ελληνική Δευτεροβάθμια Εκπαίδευση, υλοποιήσαμε μία πεντάωρη διδασκαλία στο μάθημα της Ευκλείδειας Γεωμετρίας σε Ενιαίο Ειδικό Επαγγελματικό Γυμνάσιο στην Ελλάδα. Τα παιδιά που συμμετείχαν στην έρευνα μας (4 αγόρια και 2 κορίτσια) εμφανίζουν ΕΜΔ και φοιτούν στην Γ΄ Γυμνασίου. Η διδακτική μας παρέμβαση εστίαζε στην παρουσίαση και απόδειξη μέσω της ηλεκτρονικής μορφής του Ευκλείδη του Byrne της Πρότασης Ι.5 των Στοιχείων του Ευκλείδη: «Στα ισοσκελή τρίγωνα οι γωνίες της βάσης είναι ίσες μεταξύ τους και εάν προεκταθούν οι ίσες πλευρές σχηματίζουν κάτω από τη βάση ίσες γωνίες». Για την υλοποίηση της διδακτικής μας παρέμβασης, χωρίσαμε τα παιδιά της τάξης σε δύο ομάδες. Η κάθε ομάδα διδάχθηκε την απόδειξη της Πρότασης Ι.5 με την εφαρμογή του Ευκλείδη του Byrne αλλά και με την παραδοσιακή μέθοδο διδασκαλίας.
Τα αποτελέσματα της έρευνάς μας έδειξαν ότι τα παιδιά, μέσω της χρήσης του Ευκλείδη του Byrne, κατανόησαν βασικά σημεία της απόδειξης της Πρότασης Ι.5 αλλά και βασικές έννοιες της ισότητας των τριγώνων, όπως είναι α) η εύρεση των τριγώνων που θέλουμε να εξετάσουμε ως προς την ισότητα, β) το κριτήριο που χρησιμοποιούμε για να αποδείξουμε ότι τα τρίγωνα είναι ίσα, και γ) ο εντοπισμός των κοινών στοιχείων των τριγώνων. Επίσης όλοι οι συμμετέχοντες ανέπτυξαν θετικές στάσεις για το συγκεκριμένο μάθημα.
Τα παιδιά με ΕΜΔ αποτελούν σημαντικό ποσοστό (5-15% depending on the diagnostic criteria) των παιδιών που φοιτούν σε γενικές και ειδικές σχολικές μονάδες παγκοσμίως (Grigorenko et al, 2020). Η χρήση οπτικών εφαρμογών και μέσων (όπως η χρήση βίντεο, 3D πινάκων, διδακτικών λογισμικών με χρώματα κ.ά.) μπορεί να βοηθήσει στην πιο αποτελεσματική διδασκαλία της Ευκλείδειας Γεωμετρίας σε αυτά τα παιδιά, δεδομένων των δυσκολιών που εμφανίζουν στην ανάγνωση και στην κατανόηση του γραπτού λόγου. Η έρευνα που υλοποιήσαμε συμβάλλει στην αξιοποίηση του Ευκλείδη του Byrne ως οπτικό εργαλείο διδασκαλίας της Ευκλείδειας Γεωμετρίας αλλά και στην εφαρμογή οπτικών διδακτικών παρεμβάσεων στη διδασκαλία της Ευκλείδειας Γεωμετρίας σε παιδιά με ΕΜΔ.
Θεωρητικό Πλαίσιο
2.1 Βιβλιογραφική Αναφορά
Ένα βασικό ερευνητικό ερώτημα στον χώρο της Ειδικής Εκπαίδευσης αποτελεί το πώς τα οπτικά βοηθήματα μπορεί να αποτελέσουν ένα βασικό εργαλείο για τη διδασκαλία των Μαθηματικών σε παιδιά με ΕΜΔ που αντιμετωπίζουν ιδιαίτερες δυσκολίες στην κατανόηση του γραπτού λόγου. Η χρήση του “Ευκλείδη του Byrne” στη διδασκαλία της Ευκλείδειας Γεωμετρίας φαίνεται ότι έχει θετικά αποτελέσματα στην κατανόηση γεωμετρικών εννοιών, θεωρημάτων και αξιωμάτων, όπως καταδεικνύουν σχετικές έρευνες.
Η χρήση οπτικών εφαρμογών και χρωμάτων στην διδασκαλία Μαθηματικών σε παιδιά με ΕΜΔ έχει θετικά μαθησιακά αποτελέσματα, όπως έχει επισημανθεί από διεθνείς έρευνες. Οι Kellems et al. (2020) εξέτασαν την αποτελεσματικότητα της χρήσης βίντεο βασισμένο σε μαθηματικές εντολές, χρησιμοποιώντας ασκήσεις επαυξημένης πραγματικότητας σε παιδιά δευτεροβάθμιας εκπαίδευσης με ΕΜΔ. Τα αποτελέσματα της έρευνας έδειξαν ότι όλα τα παιδιά μετά την διδακτική παρέμβαση βελτίωσαν τις μαθησιακές τους επιδόσεις σε τρείς από τις τέσσερις κατηγορίες προβλημάτων που τους δόθηκαν από τους ερευνητές.
Οι Mammarella et al. (2013) αξιολόγησαν 16 παιδιά με λεκτικές μαθησιακές δυσκολίες σε επτά περιοχές της Γεωμετρίας (Τοπολογία, Ευκλείδεια Γεωμετρία, γεωμετρικά στοιχεία, συμμετρικά στοιχεία, μετρικές σχέσεις, χειρομορφικά στοιχεία και γεωμετρικούς σχηματισμούς). Στην περιοχή της Ευκλείδειας Γεωμετρίας τα παιδιά έλαβαν μεγάλο ποσοστό σωστών απαντήσεων όταν τους χορηγήθηκαν σχήματα μεγάλου μεγέθους, αποδεικνύοντας ότι η οπτικοχωρική μνήμη είναι κρίσιμης σημασίας για την κατανόηση της Ευκλείδειας Γεωμετρίας.
Οι Soares et al. (2018) σε μία βιβλιογραφική ανασκόπηση που υλοποίησαν, μελετάνε τις ΕΜΔ και ειδικότερα τις αναγνωστικές δυσκολίες που αντιμετωπίζουν τα παιδιά, κάνοντας αναφορά σε νευρολογικές και γενετικές μελέτες, καθώς και σε νέες συμπεριφορικές και διδακτικές παρεμβάσεις που εφαρμόζονται στη διδασκαλία τους. Οι ερευνητές αναφέρουν ότι η χρήση της Τεχνολογίας είναι αποτελεσματική στη διδασκαλία των Μαθηματικών στα παιδιά με ΕΜΔ.
Μία ακόμη βιβλιογραφική ανασκόπηση που πραγματοποιήθηκε από τους Chatzivasileiou & Driga (2022), έδειξε ότι η χρήση των Τεχνολογιών Πληροφορκής και Εκπαίδευσης (ΤΠΕ), η χρήση κινητών, η χρήση Η/Υ και εκπαιδευτικών λογισμικών στη διδασκαλία των Μαθηματικών, μπορεί να βελτιώσει τη μνήμη εργασίας, την οπτική ικανότητα, τις μαθηματικές δεξιότητες και τις μεταγνωστικές δεξιότητες (όπως για παράδειγμα τη λύση προβλήματος) των παιδιών με ΕΜΔ.
Οι Bolondi & Luiqini (2018) χρησιμοποίησαν τον “Ευκλείδη του Byrne” και την εφαρμογή Geogebra για την απόδειξη προτάσεων των Στοιχείων του Ευκλείδη σε μαθητές 16 ετών σε Γυμνάσιο της Ιταλίας. Η έρευνά τους έδειξε ότι οι μαθητές μετά το πέρας της οκτάωρης διδασκαλίας ήταν σε θέση να κατανοήσουν τις αποδείξεις με τη χρήση του “Ευκλείδη του Byrne” και να παράγουν μέσω της εφαρμογής Geogebra μικροεφαρμογές για την απόδειξη της πρότασης Ι.5 των Στοιχείων: «Στα ισοσκελή τρίγωνα οι γωνίες της βάσης είναι ίσες μεταξύ τους και εάν προεκταθούν οι ίσες πλευρές σχηματίζουν κάτω από τη βάση γωνίες ίσες».
Οι Toney et al. (2013) πραγματοποίησαν μία έρευνα που σχετιζόταν με τη χρήση χρωμάτων, ως στρατηγική διδασκαλίας της Ευκλείδειας Γεωμετρίας από μια προπτυχιακή μαθηματικό που θα δίδασκε Γεωμετρία σε σχολείο Δευτεροβάθμιας Εκπαίδευσης. Τα αποτελέσματα έδειξαν ότι η χρήση χρωμάτων και τεχνικών ίδιων με αυτών που περιγράφονται στον “Ευκλείδη του Byrne” για την απόδειξη του θεωρήματος διχοτόμου μίας γωνίας (κάθε σημείο της διχοτόμου μίας γωνίας ισαπέχει από τις πλευρές της γωνίας), παρείχε ίσες ευκαιρίες σε όλους τους μαθητές, με ή χωρίς μαθησιακές δυσκολίες, να συμμετέχουν με επιτυχία στο μάθημα της Γεωμετρίας.
Οι Cass et al. (2003) πραγματοποίησαν έρευνα με αντικείμενο τη διδασκαλία προβλημάτων περιμέτρου σε μαθητές 13 ετών με ΕΜΔ. Οι ερευνητές χρησιμοποίησαν διάφορα οπτικά βοηθήματα που βασίζονταν στη χρήση χρωμάτων και χειραπτικά υλικά για τη διδασκαλία τους. Το αποτέλεσμα της έρευνας ήταν ότι οι μαθητές με τις ΕΜΔ κατάφεραν να κατανοήσουν τα είδη των τριγώνων και να τα ξεχωρίζουν.
Ωστόσο, μικρός είναι ο αριθμός των ερευνών που έχουν πραγματοποιηθεί για τη χρήση του “Ευκλείδη του Byrne” στη διδασκαλία παιδιών τυπικής ανάπτυξης. Οι Bolondi & Luiqini (2018) χρησιμοποίησαν τον “Ευκλείδη του Byrne” και την εφαρμογή Geogebra για την απόδειξη προτάσεων των Στοιχείων του Ευκλείδη σε μαθητές 16 ετών σε Γυμνάσιο της Ιταλίας. Η έρευνά τους έδειξε ότι οι μαθητές μετά το πέρας της οκτάωρης διδασκαλίας ήταν σε θέση να κατανοήσουν τις αποδείξεις με τη χρήση του “Ευκλείδη του Byrne” και να παράγουν μέσω της εφαρμογής Geogebra μικροεφαρμογές για την απόδειξη της πρότασης Ι.5 των Στοιχείων: «Στα ισοσκελή τρίγωνα οι γωνίες της βάσης είναι ίσες μεταξύ τους και εάν προεκταθούν οι ίσες πλευρές σχηματίζουν κάτω από τη βάση γωνίες ίσες».
Ο Pedeferri (2020) αναφέρει τη σημασία του “Ευκλείδη του Byrne” στη διδασκαλία της Γεωμετρίας. Πιο συγκεκριμένα, η χρήση των διαγραμμάτων και των οπτικών απεικονίσεων που υπάρχουν σ’ αυτό το έργο μπορεί να αποτελέσει πολύ σημαντικό εργαλείο διδασκαλίας της Γεωμετρίας και των Μαθηματικών γενικότερα.
Η Cirafici (2018) παρουσιάζει βασικά στοιχεία από τον “Ευκλείδη του Byrne” κι εστιάζει στην παιδαγωγική του προσέγγιση. Ειδικότερα, ερευνά το πώς η δύναμη της εικόνας και η παρουσίαση γεωμετρικών σχημάτων μπορεί να βοηθήσει τα παιδιά να συγκρατήσουν στη μνήμη τους αφηρημένες μαθηματικές έννοιες.
Απ’ όσο γνωρίζουμε υπάρχουν ελάχιστες έρευνες σχετικά με την χρήση του “Ευκλείδη του Byrne” στη διδασκαλία παιδιών με ΕΜΔ. Οι Toney et al. (2013) πραγματοποίησαν μία έρευνα που σχετιζόταν με τη χρήση χρωμάτων ως εργαλεία αναπαράστασης και κατανόησης της Ευκλείδειας Γεωμετρίας από μια προπτυχιακή μαθηματικό που θα δίδασκε Γεωμετρία σε σχολείο Δευτεροβάθμιας Εκπαίδευσης στην Αμερική. Τα αποτελέσματα έδειξαν ότι η χρήση χρωμάτων και τεχνικών ίδιων με αυτών που περιγράφονται στον “Ευκλείδη του Byrne” για την απόδειξη του θεωρήματος διχοτόμου μίας γωνίας (κάθε σημείο της διχοτόμου μίας γωνίας ισαπέχει από τις πλευρές της γωνίας), παρείχε ίσες ευκαιρίες σε όλους τους μαθητές, με ή χωρίς μαθησιακές δυσκολίες, να συμμετέχουν με επιτυχία στο μάθημα της Γεωμετρίας.
Βάσει των παραπάνω ερευνών, η χρήση οπτικών βοηθημάτων και διαφορετικών χρωμάτων για τη διδασκαλία και την απόδειξη προτάσεων της Ευκλείδειας Γεωμετρίας σε παιδιά με ΕΜΔ και σε παιδιά με τυπική ανάπτυξη φαίνεται να έχει θετικά μαθησιακά αποτελέσματα. Ο “Ευκλείδης του Byrne” αποτελεί ένα βασικό οπτικό βοήθημα, το οποίο μπορεί να χρησιμοποιηθεί για τη διδασκαλία της Ευκλείδειας Γεωμετρίας για όλους τους μαθητές με ή χωρίς μαθησιακές δυσκολίες.
Λαμβάνοντας υπόψη όλα τα παραπάνω, στην έρευνά μας θέσαμε το ακόλουθο ερευνητικό ερώτημα, το οποίο εστιάζει σε μαθητές Γ΄ Γυμνασίου με Ειδικές Μαθησιακές Δυσκολίες: Έχει η διδασκαλία των βασικών γεωμετρικών εννοιών και διαδικασιών που αξιοποιεί τον “Ευκλείδη του Byrne”, καλύτερα μαθησιακά αποτελέσματα σε σχέση με την παραδοσιακή διδασκαλία;
2.2 Η διδασκαλία της Γεωμετρίας σε Ειδικό Ενιαίο Επαγγελματικό Γυμνάσιο-Λύκειο
Το μάθημα της Γεωμετρίας στην Γ΄ Γυμνασίου διδάσκεται στην Ελλάδα μία ώρα την εβδομάδα τόσο στα Γενικά Γυμνάσια όσο και στα Ενιαία Ειδικά Επαγγελματικά Γυμνάσια. Το σχολικό εγχειρίδιο είναι μοναδικό και περιλαμβάνει, εκτός από Ευκλείδεια Γεωμετρία, βασικά στοιχεία Άλγεβρας, τα οποία διδάσκονται τρεις ώρες την εβδομάδα σε Γενικά Γυμνάσια και δύο ώρες εβδομαδιαίως σε Ενιαία Ειδικά Επαγγελματικά Γυμνάσια. Η διδασκαλία της Γεωμετρίας πραγματοποιείται βάσει του ίδιου Προγράμματος Σπουδών σε Γενικά Γυμνάσια και σε Ενιαία Ειδικά Επαγγελματικά Γυμνάσια. Η ύλη του μαθήματος καλύπτει βασικές γεωμετρικές έννοιες, προτάσεις και θεωρήματα της Ευκλείδειας Γεωμετρίας, όπως είναι η ισότητα τριγώνων, η ομοιότητα των σχημάτων, καθώς και βασικά στοιχεία τριγωνομετρίας.
Οι Clements και Battista (2013) δίνουν έναν περιεκτικό ορισμό της Ευκλείδειας Γεωμετρίας που διδάσκεται στα σχολεία, χαρακτηρίζοντάς την ως «τη μάθηση των αντικειμένων, των σχέσεων και των μετασχηματισμών του χώρου που έχουν τυποποιηθεί, και τα μαθηματικά συστήματα που έχουν δημιουργηθεί για να τα αναπαραστήσουν». Ο ορισμός αυτός ταιριάζει αρκετά με την Ελληνική σχολική πραγματικότητα. Πράγματι, ο συλλογισμός του χώρου (κυρίως του δυσδιάστατου χώρου) περιλαμβάνει γνωστικές διαδικασίες βάσει των οποίων οι νοητικές αναπαραστάσεις που χρησιμοποιούνται για την περιγραφή χωρικών αντικειμένων, σχέσεων και μετασχηματισμών, κατασκευάζονται και διαχειρίζονται από τους ίδιους τους μαθητές με την καθοδήγηση του διδάσκοντα.
Σκοπός του μαθήματος της Γεωμετρίας είναι η καλλιέργεια της λογικής σκέψης των παιδιών μέσα από την κατανόηση βασικών σχέσεων και θεωρημάτων της Ευκλείδειας Γεωμετρίας. Παράλληλα, το μάθημα στοχεύει στο να εξοικειωθούν οι μαθητές με τη λύση ασκήσεων γεωμετρίας και την κατανόηση της δομής που χρησιμοποιείται για την απόδειξη γεωμετρικών προτάσεων.
Ωστόσο, η διδασκαλία του μαθήματος της Γεωμετρίας στα Ενιαία Ειδικά Επαγγελματικά Γυμνάσια, όπως και στα Γενικά Γυμνάσια, ακολουθεί το παραδοσιακό μοντέλο διδασκαλίας. Ο εκπαιδευτικός της τάξης παρουσιάζει στον πίνακα την ύλη και στη συνέχεια οι μαθητές αντιγράφουν με “μηχανικό” τρόπο στο τετράδιό τους αυτά που βλέπουν στον πίνακα. Η μέθοδος αυτή δημιουργεί πολλές απορίες στα παιδιά με ΕΜΔ, αφού δυσκολεύονται στην κατανόηση του γραπτού λόγου και δεν αντιλαμβάνονται όσα αντιγράφουν από τον πίνακα.
Γνωρίζοντας τη συνήθη σχολική πρακτική, θεωρήσαμε ότι η διδακτική μας παρέμβαση θα μπορούσε να τραβήξει την προσοχή των μαθητών και να επιφέρει καλύτερα μαθησιακά αποτελέσματα σε σχέση με την παραδοσιακή διδασκαλία. Τα εμπειρικά ευρήματα που προέκυψαν μάλλον επιβεβαιώνουν, τουλάχιστον σε έναν βαθμό, τις διδακτικές μας επιλογές. Για παράδειγμα, ένας μαθητής που συμμετείχε στην έρευνα, δήλωσε: «Τώρα επιτέλους κατάλαβα πώς χρησιμοποιούμε το κριτήριο Π-Γ-Π και τι σημαίνει ότι δύο τρίγωνα είναι ίσα».
2.3 Στοιχεία από το Αναλυτικό Πρόγραμμα και το Σχολικό Βιβλίο
Τα προσδοκώμενα μαθησιακά αποτελέσματα για την ενότητα της Γεωμετρίας της Γ΄ Γυμνασίου που αφορά την ισότητα τριγώνων, σύμφωνα με το Πρόγραμμα Σπουδών των Μαθηματικών της Γ΄ Γυμνασίου για Γενικά Γυμνάσια αλλά και για Ενιαία Ειδικά Επαγγελματικά Γυμνάσια, είναι τα εξής: 1) οι μαθητές να είναι σε θέση να διερευνούν τον ρόλο των κριτηρίων ισότητας τριγώνων στη σύγκριση τριγώνων και να τα συσχετίζουν με τον ορισμό της ισότητας των τριγώνων, και 2) να αξιοποιούν τα κριτήρια ισότητας τριγώνων για την αιτιολόγηση ιδιοτήτων γραμμών (μεσοκαθέτου ευθύγραμμου τμήματος, διχοτόμου γωνίας κ.λπ.) και σχημάτων (π.χ. παραλληλογράμμων). Πιο συγκεκριμένα, οι μαθητές θα πρέπει να κατανοήσουν σε βάθος τη σημασία, τη χρήση των κριτηρίων ισότητας των τριγώνων, καθώς και την αξιοποίησή τους στο επίπεδο.
Επιπρόσθετα, δίνονται από το Ελληνικό Υπουργείο Παιδείας στην αρχή κάθε σχολικού έτους αναλυτικές οδηγίες διδασκαλίας για κάθε ενότητα. Οι οδηγίες αυτές, για την ενότητα της ισότητας τριγώνων, εστιάζουν στην επανάληψη βασικών γεωμετρικών γνώσεων, στην επαφή των μαθητών με πτυχές της μαθηματικής αποδεικτικής διαδικασίας, και στην επισήμανση της σπουδαιότητας των κριτηρίων ισότητας τριγώνων.
Το σχολικό εγχειρίδιο το οποίο χρησιμοποιείται για τη διδασκαλία των Μαθηματικών της Γ΄ Γυμνασίου είναι μοναδικό και παρέχεται δωρεάν από το Ελληνικό Υπουργείο Παιδείας. Αποτελείται από δύο μέρη: Το Μέρος Α, με τον τίτλο “Άλγεβρα”, περιλαμβάνει αλγεβρικές παραστάσεις, εξισώσεις, ανισώσεις και μελέτη βασικών συναρτήσεων. Το Μέρος Β, με τον τίτλο “Γεωμετρία-Τριγωνομετρία”, περιλαμβάνει ισότητα τριγώνων, λόγους μεγεθών, ομοιότητα σχημάτων και στοιχεία Τριγωνομετρίας, όπως τις βασικές τριγωνομετρικές ταυτότητες.
Πιο συγκεκριμένα, η ενότητα της ισότητας τριγώνων περιλαμβάνει ορισμένες επαναληπτικές έννοιες που αφορούν τα τρίγωνα (βασικές έννοιες, πλευρές, γωνίες, είδη τριγώνων κ.λπ.). Επιπλέον, παρατίθενται τα κριτήρια ισότητας τυχαίων και ορθογωνίων τριγώνων χωρίς τις αποδείξεις τους, καθώς και ορισμένες προτάσεις στην ισότητα των τριγώνων, πάλι χωρίς απόδειξη. Οι ασκήσεις που περιέχει η εν λόγω ενότητα είναι αποδεικτικές και εστιάζουν στην καλή γνώση των κριτηρίων της ισότητας των τριγώνων. Ο εκπαιδευτικός της τάξης έχει τη δυνατότητα να αναθέσει στους μαθητές του επιπλέον εργασία για το σπίτι που σχετίζεται με την παραπάνω ύλη.
Συνοψίζοντας τη Διαδικασία
3.1 Προκαταρκτικές Ενέργειες
Ήδη από το ακαδημαϊκό έτος 2021-2022 είχαμε την πρόθεση να υλοποιήσουμε μια ποιοτική έρευνα προκειμένου να διερευνήσουμε εάν η αξιοποίηση οπτικών βοηθημάτων στο μάθημα της Γεωμετρίας μπορεί να βοηθήσει τους μαθητές με ΕΜΔ να πετύχουν καλύτερα μαθησιακά αποτελέσματα σε σχέση με την παραδοσιακή διδασκαλία. Έτσι, τις πρώτες εβδομάδες του ακαδημαϊκού έτους 2022-2023 ο ένας από τους συγγραφείς της παρούσας εργασίας, ο οποίος διδάσκει Μαθηματικά σε μια τάξη Γ΄ Γυμνασίου σε Ενιαίο Ειδικό Επαγγελματικό Γυμνάσιο, αφιέρωσε 8 διδακτικές ώρες προκειμένου να κάνει μια γενική και σε βάθος επανάληψη επάνω στα τρίγωνα (στοιχεία και είδη τριγώνων, άθροισμα γωνιών κ.λπ.) με τους μαθητές του. Εδώ να σημειώσουμε πως στα Ενιαία Ειδικά Επαγγελματικά Γυμνάσια στην Ελλάδα υπάρχει μία επιπλέον τάξη (Δ΄ Γυμνασίου) σε σχέση με τα Γενικά Γυμνάσια, επομένως είναι στην διακριτική ευχέρεια του κάθε εκπαιδευτικού να διαχειριστεί την ύλη του μαθήματός του όπως αυτός κρίνει, ανάλογα με τις απαιτήσεις και τις ανάγκες των μαθητών του. Παράλληλα με την επανάληψη τελειοποιήσαμε τον σχεδιασμό της διδακτικής μας παρέμβασης, η υλοποίηση της οποίας άρχισε λίγες εβδομάδες αφότου ολοκληρώθηκε η επανάληψη.
3.2 Η Καθημερινή Ζωή στο Σχολείο που έγινε η έρευνα
Το Ενιαίο Ειδικό Επαγγελματικό Γυμνάσιο στο οποίο υλοποιήθηκε η έρευνα, είναι ένα σύγχρονο σχολικό συγκρότημα. Εξυπηρετεί μαθητές από όλη την περιοχή (κάπου στην κεντρική Ελλάδα) και ο Δήμος παρέχει λεωφορεία και ταξί για τις μετακινήσεις των παιδιών που έχουν εγγραφεί σε αυτό. Αποτελείται από 15 ευρύχωρες αίθουσες, οι οποίες φιλοξενούν καθημερινά 70 παιδιά ηλικίας 12 έως 18 ετών. Οι αίθουσες διαθέτουν τον κλασικό πίνακα, αλλά τα τελευταία χρόνια έχουν εφοδιαστεί και με νέους διαδραστικούς πίνακες και προτζέκτορες. Το σχολείο έχει βοηθητικές μπάρες για τα παιδιά με κινητικά προβλήματα, έτσι ώστε να διευκολύνεται η πρόσβασή τους σε όλους τους χώρους. Έχει ένα σύγχρονο εργαστήριο Πληροφορικής, εργαστήριο Ηλεκτρολογίας και εργαστήριο Γεωπονίας για τα παιδιά που ακολουθούν τον αντίστοιχο προσανατολισμό στις σπουδές τους.
Όλοι οι εκπαιδευτικοί έχουν ειδική κατάρτιση, συμμετέχουν συχνά σε επιμορφωτικές δράσεις και ανεβάζουν διδακτικό υλικό στο e-class, ενημερώνοντας παράλληλα τους μαθητές για το πώς μπορούν να μελετούν στον υπολογιστή τους το υλικό αυτό. Οι περιπτώσεις των παιδιών που φοιτούν στο συγκεκριμένο σχολείο είναι αντιπροσωπευτικές των παιδιών που φοιτούν σε Ενιαία Ειδικά Επαγγελματικά Γυμνάσια σε όλη τη χώρα. Πιο συγκεκριμένα, στο σχολείο φοιτούν παιδιά στο φάσμα του αυτισμού, παιδιά με ΕΜΔ, παιδιά με κινητικά προβλήματα, παιδιά με ήπια και μέτρια νοητική καθυστέρηση κ.λπ. Στο σχολείο υπάρχει φιλικό κλίμα μεταξύ όλων των μαθητών αλλά και μεταξύ μαθητών και εκπαιδευτικών.
3.3. Τα παιδιά που συμμετείχαν
Το τμήμα της Γ΄ Γυμνασίου που συμμετείχε στην έρευνά μας αποτελείται από 6 παιδιά (4 αγόρια και 2 κορίτσια). Τα παιδιά προέρχονται από το ίδιο πολιτισμικό περιβάλλον και τα γνωρίζουμε προσωπικά από την προηγούμενη σχολική χρονιά. Πιο συγκεκριμένα (χρησιμοποιούμε ψευδώνυμα προκειμένου να διαφυλάξουμε την ανωνυμία των παιδιών):
Ο Πάνος είναι 15 ετών και έχει κατακτήσει βασικές γεωμετρικές δεξιότητες. Ωστόσο, δυσκολεύεται στην ανάκληση προηγούμενης μαθηματικής γνώσης όταν αυτή απαιτείται για την επίλυση ασκήσεων.
Η Μαρία είναι 15 ετών και έχει κατακτήσει βασικές γνώσεις Γεωμετρίας. Δυσκολεύεται στην αναγνώριση γεωμετρικών σχημάτων και σχέσεων.
Ο Θάνος είναι 16 ετών, έχει χαμηλό μαθηματικό υπόβαθρο και δυσκολεύεται να συγκεντρωθεί στο μάθημα. Δυσκολεύεται να κατανοήσει βασικές γεωμετρικές σχέσεις και να τις ανακαλέσει στην μνήμη του.
Η Ιωάννα είναι 15 χρονών και το μαθηματικό της υπόβαθρο είναι αρκετά χαμηλό. Γνωρίζει τα βασικά γεωμετρικά σχήματα αλλά δυσκολεύεται να τα σχεδιάσει.
Ο Γρηγόρης είναι 16 ετών και έχει ένα καλό μαθηματικό υπόβαθρο. Μπορεί να κατανοήσει βασικές γεωμετρικές σχέσεις και να σχεδιάσει γεωμετρικά σχήματα.
Ο Κώστας είναι 15 ετών και έχει ένα καλό μαθηματικό επίπεδο. Ξέρει να σχεδιάζει σχήματα και μπορεί να απομνημονεύσει μαθηματικές σχέσεις.
Επιπλέον, όλοι δυσκολεύονται να αντιγράψουν στο τετράδιό τους αυτά που βλέπουν στον πίνακα. Πιο συγκεκριμένα, αντιμετωπίζουν δυσκολίες στην κατανόηση των μαθηματικών συμβόλων και στην κατανόηση του περιεχομένου αυτών που αντιγράφουν.
Η διδακτική παρέμβαση
Τον Δεκέμβριο του 2022 πραγματοποιήσαμε μία πεντάωρη διδασκαλία σε ένα από τα δύο τμήματα της Γ΄ Γυμνασίου ενός Ενιαίου Ειδικού Επαγγελματικού Γυμνασίου με κύριο θέμα τη διδασκαλία της Πρότασης Ι.5 των Στοιχείων του Ευκλείδη: «Στα ισοσκελή τρίγωνα οι γωνίες της βάσης είναι ίσες μεταξύ τους και εάν προεκταθούν οι ίσες πλευρές σχηματίζουν κάτω από τη βάση γωνίες ίσες» που εντάσσεται στην ενότητα «Ισότητα τριγώνων» του σχολικού εγχειριδίου, με τη χρήση του Ευκλείδη του Byrne, και τη σύγκριση του Ευκλείδη του Byrne με την παραδοσιακή μέθοδο διδασκαλίας που εφαρμόζεται στο σχολείο.
Την πρώτη ώρα της πεντάωρης διδασκαλίας, παρουσιάστηκε σύντομα στον διαδραστικό πίνακα η ηλεκτρονική μορφή του Ευκλείδη του Byrne. Επιπλέον, έγινε και ο χωρισμός των μαθητών σε δύο ομάδες με τυχαίο τρόπο. Η πρώτη ομάδα θα διδασκόταν την Πρόταση Ι.5 των Στοιχείων με την παραδοσιακή μέθοδο διδασκαλίας στον μαυροπίνακα, ενώ η άλλη ομάδα θα διδασκόταν την ίδια πρόταση με τη χρήση του Ευκλείδη του Byrne.
Όταν έγινε η σύντομη παρουσίαση του Ευκλείδη του Byrne, όλα τα παιδιά εντυπωσιάστηκαν. Πιο συγκεκριμένα, τα παιδιά ενθουσιάστηκαν με τη χρήση των διαφορετικών χρωμάτων που χρησιμοποιούνται για την απεικόνιση των πλευρών και των γωνιών των τριγώνων. Ο χωρισμός των ομάδων αποδείχθηκε λοιπόν μια δύσκολη διαδικασία, καθώς όλοι οι μαθητές και οι μαθήτριες ήθελαν να συμμετάσχουν στην ομάδα που θα αποδείκνυε την πρόταση με τη χρήση του Ευκλείδη του Byrne. Για τον λόγο αυτό, ανακοινώσαμε στα παιδιά ότι μετά το τέλος της διδασκαλίας θα γίνει αντιστροφή των ομάδων και τα παιδιά που θα διδασκόντουσαν την Πρόταση Ι.5 των Στοιχείων με την παραδοσιακή διδασκαλία, θα την διδασκόντουσαν στη συνέχεια και με τη χρήση του Ευκλείδη του Byrne, και αντίστροφα για την άλλη ομάδα. Έτσι, η τρίωρη διδασκαλία που είχαμε προγραμματίσει αρχικά, έγινε πεντάωρη. Οι ομάδες λοιπόν χωρίστηκαν ως εξής:
Α΄ Ομάδα: Ο Πάνος, η Μαρία και ο Θάνος, οι οποίοι θα διδασκόντουσαν την Πρόταση Ι.5 με τη χρήση του Ευκλείδη του Byrne.
Β΄ Ομάδα: Η Ιωάννα, ο Γρηγόρης και ο Κώστας, οι οποίοι θα διδασκόντουσαν την Πρόταση Ι.5 με την παραδοσιακή μέθοδο διδασκαλίας.
Image 1. Proposition I.5, exactly as presented in Byrne’s Euclid

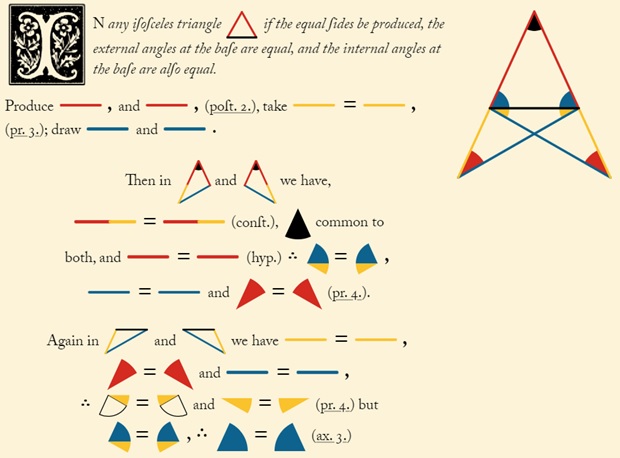
Τη δεύτερη ώρα της διδακτικής μας παρέμβασης, πραγματοποιήθηκε η διδασκαλία της πρότασης Ι.5 των Στοιχείων στην Ομάδα Α. Αρχικά, παρουσιάσαμε στον διαδραστικό πίνακα την πρόταση αξιοποιώντας τον Ευκλείδη του Byrne (see Image 1). Τα παιδιά κατανόησαν το περιεχόμενο της πρότασης και αυτό που καλούμαστε να αποδείξουμε, χωρίς να εκφράσουν καμία απολύτως απορία. Πιο συγκεκριμένα, οι μαθητές της Ομάδας Α κατάλαβαν το περιεχόμενο της πρότασης και ποιες γωνίες θέλουμε να αποδείξουμε ότι είναι ίσες από τα χρώματα, τα οποία αντικαθιστούν τα λόγια και τα γεωμετρικά σύμβολα που χρησιμοποιούνται σε προτάσεις στη Γεωμετρία. Μάλιστα, η Μαρία σήκωσε το χέρι της με έντονο τρόπο και με ένα μεγάλο χαμόγελο μας είπε: «Κύριε είναι η πρώτη φορά που καταλαβαίνω κατευθείαν τι πρέπει να αποδείξω στη Γεωμετρία εξαιτίας των χρωμάτων που υπάρχουν και δεν χρειάζεται να διαβάσω πολλές φορές την πρόταση που πρέπει να αποδείξουμε για να καταλάβω τι πρέπει να κάνουμε».
Και τα υπόλοιπα παιδιά της Ομάδας Α παρακολουθούσαν με έντονο εντυπωσιασμό και απόλυτη συγκέντρωση την παρουσίαση της πρότασης. Όταν προχωρήσαμε στην απόδειξή της, όλα τα παιδιά κατανόησαν ποια τρίγωνα πρέπει να συγκρίνουμε αρχικά, χρησιμοποιώντας το κριτήριο «Πλευρά-Γωνία-Πλευρά» (Π-Γ-Π). Πιο συγκεκριμένα, όταν μετακινούσαμε το ποντίκι του υπολογιστή στα τρίγωνα που πρέπει να συγκρίνουμε και τα στοιχεία τους που ήταν ίσα παρουσιάζονταν με τα ίδια χρώματα, όλα τα παιδιά της ομάδας έδειξαν έντονο ενθουσιασμό γιατί κατανόησαν πλήρως γιατί τα τρίγωνα που συγκρίναμε είναι ίσα. Στο πλαίσιο αυτό, ο Πάνος είπε με χαρά και έντονο συναίσθημα αυτοπεποίθησης: «Τώρα επιτέλους κατάλαβα πώς χρησιμοποιούμε το κριτήριο Π-Γ-Π και τι σημαίνει πως δύο τρίγωνα είναι ίσα. Κατάλαβα την έννοια της κοινής γωνίας δύο τριγώνων τώρα που την δείξατε με τα χρώματα».
Ολοκληρώνοντας την απόδειξη, χρειάστηκε να συγκρίνουμε δύο ακόμη τρίγωνα για να αποδείξουμε ότι είναι ίσα και να καταλήξουμε στο ζητούμενο. Τα παιδιά κατάλαβαν τα στοιχεία που έχουν τα τρίγωνα έτσι ώστε να είναι ίσα με τη βοήθεια των χρωμάτων, και χρησιμοποιώντας το κριτήριο του Π-Γ-Π οδηγηθήκαμε στο πέρας της απόδειξης της πρότασης. Όταν ολοκληρώθηκε η απόδειξη, ο Θάνος με μεγάλη προέκταση του χεριού του, που δήλωνε ικανοποίηση, είπε: «Θα ήθελα από εδώ και στο εξής όλα τα μαθήματα Γεωμετρίας που θα κάνουμε να γίνονται στον διαδραστικό πίνακα με τον Ευκλείδη του Byrne».
Την τρίτη ώρα πραγματοποιήθηκε η διδασκαλία της πρότασης Ι.5 των Στοιχείων στην Ομάδα Β με την παραδοσιακή μέθοδο. Αρχικά, παρουσιάσαμε στον μαυροπίνακα την πρόταση αντιγράφοντας την εκφώνηση από το σχολικό εγχειρίδιο και κάνοντας ένα σχήμα με τη χρήση γεωμετρικού οργάνου (χάρακα). Οι μαθητές καθώς αντέγραφαν την πρόταση στο τετράδιό τους, δυσκολεύτηκαν στην κατανόηση του περιεχομένου της, καθώς και στο τι θέλουμε να αποδείξουμε. Ο Κώστας με βλέμμα γεμάτο απορία ρώτησε: «Κύριε δεν μπορώ να καταλάβω τι θέλουμε να αποδείξουμε. Ποιες είναι οι γωνίες κάτω από τη βάση και πώς θα προεκτείνουμε τις πλευρές από μόνοι μας;».
Στη συνέχεια δείξαμε στα παιδιά ποια τρίγωνα πρέπει να συγκρίνουμε, αρχικά, για να δούμε αν είναι ίσα ή όχι. Τα παιδιά δυσκολεύτηκαν να εντοπίσουν στον πίνακα ποια στοιχεία των τριγώνων που συγκρίναμε ήταν ίσα. Επίσης, τα παιδιά δυσκολεύτηκαν να εντοπίσουν από μόνα τους ποια τρίγωνα πρέπει να συγκρίνουν, με αποτέλεσμα να απογοητευτούν. Μάλιστα, ο Κώστας και η Ιωάννα έπιασαν το κεφάλι τους, αφού δεν μπορούσαν να κατανοήσουν αυτά που αντέγραφαν από τον πίνακα. Η Ιωάννα με φωνή σιγανή και με μικρή προέκταση του χεριού της είπε: «Κύριε δεν έχω καταλάβει τίποτα. Δυσκολεύομαι πολύ να διαβάσω από τον πίνακα τα τρίγωνα που πρέπει να συγκρίνουμε και να βρω ποια στοιχεία τους είναι ίδια».
Όταν προχωρήσαμε στην τελευταία σύγκριση των τριγώνων για να καταλήξουμε στο ζητούμενο της απόδειξης, οι μαθητές της τάξης μπερδεύτηκαν σε μεγάλο βαθμό. Πιο συγκεκριμένα, δεν μπορούσαν να βρουν τα τρίγωνα που έπρεπε να συγκρίνουν, αφού στο σχήμα που υπήρχε στον πίνακα υπήρχαν και τα προηγούμενα τρίγωνα που είχαμε συγκρίνει. Επιπλέον, δυσκολεύτηκαν να βρουν τα στοιχεία που χρειαζόντουσαν για να αποδείξουν ότι τα τρίγωνα είναι ίσα, με αποτέλεσμα να αποθαρρυνθούν.
Όταν ολοκληρώθηκε η απόδειξη, τα παιδιά κοιτούσαν το ρολόι τους επίμονα για να δουν πότε θα χτυπήσει το κουδούνι. Ρωτήσαμε τα παιδιά αν είχαν κατανοήσει την απόδειξη της πρότασης και οι απαντήσεις που πήραμε ήταν απογοητευτικές. Ο Γρηγόρης σκυμμένος μπροστά από το θρανίο του με πολύ σιγανή φωνή μας είπε: «Κύριε δεν καταλαβαίνω καθόλου τη Γεωμετρία. Αυτά που γράφουμε στον πίνακα είναι δύσκολα και δεν μπορώ να τα καταλάβω παρόλο που τα διαβάζω πολλές φορές στο σπίτι μου».
Την τέταρτη ώρα της διδακτικής μας παρέμβασης, έγινε η αλλαγή του δυναμικού των ομάδων, εφόσον τα παιδιά της ομάδας Β αφού διδάχθηκαν την πρόταση με την παραδοσιακή μέθοδο διδασκαλίας το ξαναζήτησαν επίμονα. Οι ομάδες τώρα έγιναν:
Α΄ Ομάδα: Η Ιωάννα, ο Γρηγόρης και ο Κώστας, οι οποίοι θα διδασκόντουσαν την Πρόταση Ι.5 με τον Ευκλείδη του Byrne.
Β΄ Ομάδα: Ο Πάνος, η Μαρία και ο Θάνος οι οποίοι θα διδασκόντουσαν την Πρόταση Ι.5 με την παραδοσιακή μέθοδο.
Παρουσιάστηκε η πρόταση Ι.5 των Στοιχείων με τη χρήση του Ευκλείδη του Byrne στον διαδραστικό πίνακα στη νέα ομάδα Α, η οποία είχε διδαχθεί την εν λόγω πρόταση με την παραδοσιακή μέθοδο διδασκαλίας πριν λίγες μέρες. Οι μαθητές μόλις είδαν τα χρώματα αντί των γραμμάτων και των γεωμετρικών συμβόλων ενθουσιάστηκαν και κατανόησαν αυτή τη φορά το περιεχόμενο της πρότασης καθώς και όλα τα στάδια της απόδειξής της, χωρίς να εκφράσουν δυσκολίες στην κατανόηση της πρότασης και απορίες σχετικά με την απόδειξη. Πιο συγκεκριμένα, τα παιδιά μάς ζήτησαν η διδασκαλία της Γεωμετρίας να γίνεται με τον Ευκλείδη του Byrne, αφού μπόρεσαν να εντοπίσουν κατευθείαν τα τρίγωνα που πρέπει να συγκρίνουν και τα στοιχεία που χρειάζονταν για να αποδείξουν ότι τα τρίγωνα είναι ίσα μεταξύ τους.
Ο Γρηγόρης γεμάτος πλέον με χαρά και αυτοπεποίθηση σηκώνοντας το χέρι του πολύ ψηλά είπε: «Κύριε μπορούμε να χρησιμοποιούμε χρώματα και στην Άλγεβρα; Το χρώμα μάς διευκολύνει να καταλάβουμε αυτά που μας λέτε χωρίς να δυσκολευόμαστε». Τα υπόλοιπα παιδιά της ομάδας είχαν πλέον χαρούμενα πρόσωπα και είχαν αποβάλλει το άγχος και την απογοήτευση που είχαν στην απόδειξη της πρότασης με την παραδοσιακή μέθοδο διδασκαλίας.
Την πέμπτη ώρα, παρουσιάστηκε στα παιδιά της ομάδας Β η απόδειξη της πρότασης Ι.5 των Στοιχείων με την παραδοσιακή μέθοδο διδασκαλίας, ενώ τα ίδια την είχαν διδαχθεί με τον Ευκλείδη του Byrne. Τα παιδιά κατανόησαν σχετικά εύκολα το περιεχόμενο της πρότασης, επειδή το θυμόντουσαν από τη διδασκαλία της ίδιας πρότασης με τη χρήση του Ευκλείδη του Byrne που πραγματοποιήθηκε πριν λίγες μέρες. Στην συνέχεια, καθώς αποδεικνύαμε την πρόταση, υπήρχαν δυσκολίες κατά τη διάρκεια της αντιγραφής από τον πίνακα αλλά τα παιδιά θυμόντουσαν σε ικανοποιητικό βαθμό τα τρίγωνα που έπρεπε να συγκρίνουν καθώς και τα στοιχεία των τριγώνων που έπρεπε να βρουν από την απόδειξη της ίδιας πρότασης με την χρήση του Ευκλείδη του Byrne. Στο τέλος της διδασκαλίας, τα παιδιά μας ζήτησαν να μην ξαναχρησιμοποιήσουμε τον πίνακα και την κλασσική μέθοδο διδασκαλίας στη Γεωμετρία γιατί τους προκαλεί σύγχυση και άγχος, και δεν μπορούν να κατανοήσουν αυτά που γράφουμε στον πίνακα.
Μάλιστα, η Μαρία χαμογελώντας αλλά ταυτόχρονα και με ένα αίσθημα ανησυχίας και άγχους, είπε: «Κύριε ευτυχώς που πριν δύο μέρες μάς δείξατε την πρόταση αυτή με χρώματα στον διαδραστικό πίνακα, αλλιώς δεν θα καταλάβαινα τίποτα. Τα διαφορετικά χρώματα με βοήθησαν να θυμηθώ τα στοιχεία των τριγώνων που είναι ίσα και τα τρίγωνα που έπρεπε να συγκρίνουμε». Με την Μαρία συμφώνησαν και τα υπόλοιπα μέλη της ομάδας και κατέληξαν στο ότι ο Ευκλείδης του Byrne ήταν πολύ βοηθητικός στη διδασκαλία, αφού δεν χρειάστηκε να διαβάσουν κείμενο και να αντιγράψουν από τον μαυροπίνακα.
Τέλος, είχαμε μια συζήτηση μικρής διάρκειας (5-7 λεπτών μέχρι να χτυπήσει το κουδούνι και να ολοκληρωθεί η πέμπτη και τελευταία ώρα της διδασκαλίας μας) με όλα τα παιδιά του τμήματος σχετικά με την πρόταση και την απόδειξή της. Όλα τα παιδιά υποστήριξαν με κατηγορηματικό τρόπο ότι η χρήση του Ευκλείδη του Byrne για τη διδασκαλία της Γεωμετρίας τα διευκόλυνε στην κατανόηση του περιεχομένου της πρότασης και της απόδειξής της, και θα ήθελαν να χρησιμοποιείται από εδώ και πέρα σε όλα τα μαθήματα Γεωμετρίας που θα ακολουθήσουν. Επιπλέον, ρώτησαν αν υπάρχει αντίστοιχο οπτικό βοήθημα και στην Άλγεβρα προκειμένου να το χρησιμοποιήσουν και εκεί.
Η έρευνα που υλοποιήσαμε στο τμήμα της Γ΄ Γυμνασίου είναι ποιοτική και στοχεύει να μελετήσει σε βάθος τα αποτελέσματα της διδασκαλίας σε παιδιά με ΕΜΔ αξιοποιώντας τον Ευκλείδη του Byrne. Επομένως, η μεθοδολογία που θεωρήθηκε κατάλληλη προκειμένου να απαντηθεί το ερευνητικό ερώτημα που θέσαμε, ήταν εκείνη η οποία βασίζονταν σε ανοιχτές ερωτήσεις (οι οποίες περιλαμβάνονται σε ερωτηματολόγιο που κατασκευάσαμε) και απαντήθηκαν από τα παιδιά, ώστε να έρθει στην επιφάνεια τι σκέφτονται και γιατί.
Ανάλυση των Δεδομένων της Έρευνας
Τα βασικά δεδομένα της έρευνάς μας (πέρα από τις παρατηρήσεις που κάναμε κατά τη διάρκεια των μαθημάτων), αντλήθηκαν από ερωτηματολόγιο το οποίο τα παιδιά κλήθηκαν να απαντήσουν προφορικά, λόγω των δυσκολιών που αντιμετωπίζουν στον γραπτό λόγο. Το ερωτηματολόγιο απαρτιζόταν από τρείς ερωτήσεις ανοιχτού τύπου, που το κάθε παιδί καλούνταν να απαντήσει μόνο του με την παρουσία του δασκάλου στην τάξη. Οι ερωτήσεις του ερωτηματολογίου ήταν οι εξής:
Q1. Ποια σημεία από τον “Ευκλείδη του Byrne” σας έκαναν ιδιαίτερη εντύπωση (θετική ή αρνητική) κατά τη διάρκεια της διδασκαλίας;
Q2. Την έννοια της ισότητας των τριγώνων και το κριτήριο ισότητας των τριγώνων «Πλευρά- Γωνία-Πλευρά» που εμπεριέχονται στην απόδειξη της Πρότασης που διδαχθήκατε, τα κατανοήσατε πιο εύκολα μέσα από τη διδασκαλία που βασίστηκε στον “Ευκλείδη του Byrne” ή μέσα από την παραδοσιακή μέθοδο διδασκαλίας (δηλαδή αυτή που συνηθίζουμε να ακολουθούμε στην τάξη);
Q3. Θα προτιμούσατε τον “Ευκλείδη του Byrne” ή την παραδοσιακή μέθοδο διδασκαλίας για τη διδασκαλία του μαθήματος της Γεωμετρίας και για ποιο λόγο;
Αφού υλοποιήσαμε τις ημιδομημένες συνεντεύξεις με τα παιδιά, συλλέξαμε τα δεδομένα και προχωρήσαμε στην ανάλυσή τους. Για την ανάλυση των δεδομένων χρησιμοποιήσαμε τη μέθοδο της ανάλυσης περιεχομένου (Abreu et al., 2022). Πιο συγκεκριμένα, προχωρήσαμε σε μία αρχική κωδικοποίηση των δεδομένων που προκύπτουν από τις συνεντεύξεις των παιδιών.
Table 1. Q1-Which parts of Byrne’s Euclid made a particular impression on you during the lesson?
Αποσπάσματα συνεντεύξεων | Κωδικοί |
Κώστας: Η χρήση των χρωμάτων που είδα στις πλευρές και στις κορυφές των τριγώνων στον διαδραστικό πίνακα, μου έκανε θετική εντύπωση. Τα χρώματα με βοήθησαν να καταλάβω ποια τρίγωνα θα συγκρίνω, τις ίσες πλευρές και γωνίες. […] Τα λόγια και οι εκφωνήσεις πάντα με μπέρδευαν στα Μαθηματικά και δεν ήξερα ποτέ τι πρέπει να κάνω. Τώρα καταλαβαίνω τι μου ζητάει η απόδειξη. | Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne
Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων |
Θάνος: Επιτέλους κατάλαβα τι πρέπει να κάνω. Ουφφφ μου έφυγε το άγχος που είχα όταν είχαμε Μαθηματικά και γράφαμε συνέχεια στον πίνακα. Πλέον καταλαβαίνω τι πρέπει να κάνω στις ασκήσεις που κάνουμε, αφού τα λόγια πάντα με μπέρδευαν. Μακάρι να χρησιμοποιούσαμε τον Ευκλείδη του Byrne και στην Άλγεβρα. Οι χρωματισμένες πλευρές και γωνίες με βοήθησαν να καταλάβω τι σημαίνει προέκταση των πλευρών ενός τριγώνου που μας εξηγούσατε στον πίνακα με τον μαρκαδόρο. |
Αρνητικό συναίσθημα του παιδιού για τα Μαθηματικά με την παραδοσιακή διδασκαλία
Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων
Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne |
Γρηγόρης: Σίγουρα τα χρώματα που είδα στα σχήματα στον πίνακα με βοήθησαν. Όταν είχαμε Μαθηματικά και ο δάσκαλος έγραφε στον πίνακα με μαρκαδόρο, δεν καταλάβαινα τα γράμματα και τα σχήματα από τον πίνακα. Δηλαδή δεν καταλάβαινα ποιες πλευρές έπρεπε να βρω και ποιες γωνίες. Και αγχωνόμουν πολύ. Πάρα πολύ. Όταν μας δείξατε την απόδειξη με τον Ευκλείδη του Byrne, κατάλαβα τι πρέπει να βρούμε και τι πρέπει να κάνουμε. Επίσης, κατάλαβα τι εννοούμε όταν λέμε πλευρά του τριγώνου και γωνία του τριγώνου, αφού με τα χρώματα όλα ήταν ξεκάθαρα. | Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων Αρνητικό συναίσθημα του παιδιού για τα Μαθηματικά με την παραδοσιακή διδασκαλία
Κατανόηση βασικών γεωμετρικών εννοιών |
Μαρία: Αρχικά, δεν υπάρχουν τύποι και γράμματα στον πίνακα. Πάντα με δυσκόλευε να τα αντιγράφω αυτά από τον πίνακα. Ο διαδραστικός πίνακας μου αρέσει πολύ, γιατί όλα φαίνονται πιο εύκολα. Τα Μαθηματικά είναι ένα μάθημα που με ενδιαφέρει και τα χρώματα που είδα στην απόδειξη ήταν πολύ βοηθητικά. | Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων Θετική επίδραση των ΤΠΕ στη διδασκαλία παιδιών με ΕΜΔ Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne |
Ιωάννα: Τα Μαθηματικά είναι ένα μάθημα που με δυσκολεύει πολύ. Ειδικά στη Γεωμετρία δεν μπορούσα να καταλάβω ποια είναι η διαφορά της γωνίας από την πλευρά και τους συμβολισμούς που χρησιμοποιεί ο δάσκαλος στον πίνακα. Μόλις όμως μας έδειξε τα τρίγωνα με χρώματα και χωρίς γράμματα, όλα έγιναν πιο εύκολα. Κατάλαβα τη διαφορά πλευράς-γωνίας και τι σημαίνει προέκταση πλευράς. Πολλές φορές ο δάσκαλος είχε γράψει αυτή τη λέξη στον πίνακα αλλά ποτέ δεν κατάλαβα τι σημαίνει πραγματικά. Θέλω να χρησιμοποιούμε συνέχεια τον Ευκλείδη του Byrne και τον διαδραστικό πίνακα γιατί έτσι θα καταλαβαίνω πιο εύκολα τη Γεωμετρία. Μακάρι να υπήρχε και ένα τέτοιο βοήθημα και στην Άλγεβρα. |
Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων Κατανόηση γεωμετρικών εννοιών με την χρήση χρωμάτων μέσω του Ευκλείδη του Byrne Κατανόηση βασικών γεωμετρικών εννοιών Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων Θετική επίδραση των ΤΠΕ στη διδασκαλία παιδιών με ΕΜΔ |
Πάνος: Δεν βρίσκω τίποτα αρνητικό στον Ευκλείδη του Byrne που χρησιμοποιήσαμε στο μάθημα. Τα χρώματα που χρησιμοποιούνται για να συμβολίσουμε γωνίες και πλευρές είναι πολύ βοηθητικά για να καταλάβω ποια τρίγωνα πρέπει να συγκρίνω και ποια στοιχεία τους είναι ίσα. Θα ήθελα επίσης να χρησιμοποιούμε και μια αντίστοιχη μέθοδο και στην Άλγεβρα για να καταλάβουμε και εκεί τις μαθηματικές σχέσεις που κάνουμε. Με αγχώνουν πολύ τα γράμματα και τα σύμβολα που χρησιμοποιούμε και στην Άλγεβρα και στην Γεωμετρία. Με αγχώνει πολύ αυτή η διαδικασία. |
Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne
Θετική επίδραση των ΤΠΕ στη διδασκαλία παιδιών με ΕΜΔ Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων Αρνητικό συναίσθημα του παιδιού για τα Μαθηματικά με την παραδοσιακή διδασκαλία |
Table 2. Q2-Did you understand the concept of equality of triangles and the criterion of equality of triangles “Side-Angle-Side” contained in the proof of the Proposition you were taught more easily through the teaching based on “Byrne’s Euclid” or through the traditional teaching method (i.e. the one we usually follow in the classroom)?
Αποσπάσματα συνεντεύξεων | Κωδικοί |
Κώστας: Σίγουρα με τον Ευκλείδη του Byrne […] Παλιότερα δεν είχα καταλάβει το κριτήριο “Πλευρά-Γωνία-Πλευρά”, δεν είχα καταλάβει τι σημαίνει περιεχόμενη γωνία και πώς μπορώ να την βρω στο σχήμα. Τα χρώματα που υπάρχουν στον Ευκλείδη του Byrne με βοήθησαν να καταλάβω πώς μπορώ να εντοπίσω τα στοιχεία των τριγώνων που θέλω να συγκρίνω, αλλά και την έννοια της περιεχόμενης γωνίας. Παλιότερα ήμουν αγχωμένος γιατί δεν μπορούσα να τα κατανοήσω από τον πίνακα. Πιστεύω ότι τη Γεωμετρία θα πρέπει να την κάνουμε με τον Ευκλείδη του Byrneκαι με τη χρήση διαδραστικού πίνακα. Οι εικόνες και τα χρώματα με βοηθούν πάρα πολύ να καταλάβω. |
Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων
Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne
Αρνητικό συναίσθημα του παιδιού για τα Μαθηματικά με την παραδοσιακή διδασκαλία
Θετική επίδραση των ΤΠΕ στη διδασκαλία παιδιών με ΕΜΔ |
Θάνος: Με τον Ευκλείδη του Byrne […] Πριν μας δείξετε την απόδειξη με τον Ευκλείδη του Byrne, δεν μπορούσα να κατανοήσω τα βασικά της Γεωμετρίας, όπως για παράδειγμα τι σημαίνει ότι προεκτείνουμε μία πλευρά. […] |
Κατανόηση βασικών γεωμετρικών εννοιών |
Γρηγόρης: Το κριτήριο Πλευρά-Γωνία-Πλευρά δεν το είχα καταλάβει πολύ καλά στον πίνακα. Αυτό ήταν κάτι που με στεναχωρούσε γιατί πιστεύω ότι είμαι καλός στη Γεωμετρία […] Με δυσκόλευαν οι συμβολισμοί των τριγώνων και των γωνιών γιατί αυτοί μοιάζουν μεταξύ τους. […] Ο διαδραστικός πίνακας πρέπει να χρησιμοποιείται για τη διδασκαλία και της Γεωμετρίας και της Άλγεβρας. |
Αρνητικό συναίσθημα του παιδιού για τα Μαθηματικά με την παραδοσιακή διδασκαλία Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων Θετική επίδραση των ΤΠΕ στη διδασκαλία παιδιών με ΕΜΔ |
Μαρία: Με πολύ χαρά σας λέω ότι αυτό που με βοήθησε να καταλάβω ήταν ο Ευκλείδης του Byrne. Κατάλαβα αρχικά ποια είναι τα τρίγωνα που έπρεπε να συγκρίνω, επειδή τα χρώματα μου τα υπέδειξαν και επίσης κατάλαβα τα στοιχεία που έχουν ίσα. […] Όταν δεν καταλαβαίνω τι πρέπει να κάνω, αγχώνομαι και στενοχωριέμαι. | Συναισθήματα χαράς και αυτοπεποίθησης από τη χρήση του Ευκλείδη του Byrne
Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne
Αρνητικό συναίσθημα του παιδιού για τα Μαθηματικά με την παραδοσιακή διδασκαλία |
Ιωάννα: Όταν κάναμε ασκήσεις και αποδείξεις στον πίνακα [με την παραδοσιακή μέθοδο διδασκαλίας], τα γράμματα και οι σχέσεις με μπέρδευαν και δεν μπορούσα να καταλάβω τη σημασία τους. Ο Ευκλείδης του Byrne με βοήθησε να καταλάβω άμεσα αυτά που βλέπω στον διαδραστικό πίνακα. Τα χρώματα με βοήθησαν να βρω ποια τρίγωνα πρέπει να συγκρίνω και τα στοιχεία που είναι ίσα. Επομένως αυτός ο τρόπος [ο Ευκλείδης του Byrne] είναι πολύ πιο αποτελεσματικός από αυτά που κάναμε παλιά. Τώρα χαίρομαι την ώρα των Μαθηματικών. |
Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων Θετική επίδραση των ΤΠΕ στη διδασκαλία παιδιών με ΕΜΔ Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne
Συναισθήματα χαράς και αυτοπεποίθησης από τη χρήση του Ευκλείδη του Byrne |
Πάνος: Εννοείται [καλύτερη μέθοδος είναι] ο Ευκλείδης του Byrne. Χωρίς δεύτερη σκέψη. Αρχικά, τα χρώματα με βοήθησαν να καταλάβω ποια τρίγωνα πρέπει να συγκρίνω και επίσης να καταλάβω τι σημαίνει το κριτήριο Πλευρά-Γωνία-Πλευρά. […] Η αντιγραφή από τον πίνακα με δυσκολεύει, τώρα όμως δεν είναι απαραίτητη. | Συναισθήματα χαράς και αυτοπεποίθησης από τη χρήση του Ευκλείδη του Byrne Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων |
Table 3. Q3-Would you prefer Byrne’s Euclid or the traditional method of teaching Geometry and why?
Αποσπάσματα συνεντεύξεων | Κωδικοί |
Κώστας: Σίγουρα θα επέλεγα τον Ευκλείδη του Byrne για τη διδασκαλία της Γεωμετρίας. Ο λόγος είναι ότι τα χρώματα που είχε η απόδειξη, με βοήθησε να την καταλάβω χωρίς ιδιαίτερη δυσκολία. Επίσης, ο Ευκλείδης του Byrne δεν έχει λόγια και μαθηματικά σύμβολα που πολλές φορές με μπερδεύουν και στεναχωριέμαι γι’ αυτό. | Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων Αρνητικό συναίσθημα του παιδιού για τα Μαθηματικά με την παραδοσιακή διδασκαλία |
Θάνος: [Θα επέλεγα] τον Ευκλείδη του Byrne. Με βοήθησε να καταλάβω και να λύσω βασικές απορίες που είχα στη Γεωμετρία, όπως τι σημαίνει περιεχόμενη γωνία και γενικότερα απορίες που είχα στα τρίγωνα. Ακόμη, τα χρώματα με βοήθησαν να βρω τα τρίγωνα που πρέπει να συγκρίνω, χωρίς να μπερδευτώ. |
Κατανόηση βασικών γεωμετρικών εννοιών
Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne |
Γρηγόρης: Είμαι ενθουσιασμένος με τον Ευκλείδη του Byrne. Θα ήθελα όλα τα μαθήματα από εδώ και στο εξής στη Γεωμετρία να τα κάνουμε έτσι. […] Υπάρχουν πολλά θετικά σημεία. Δεν γράφουμε στον πίνακα σύμβολα και λόγια. Αυτά με δυσκολεύουν. […] Μακάρι να υπήρχε και κάτι παρόμοιο και στην Άλγεβρα. | Συναισθήματα χαράς και αυτοπεποίθησης από τη χρήση του Ευκλείδη του Byrne Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων Αρνητικό συναίσθημα του παιδιού για τα Μαθηματικά με την παραδοσιακή διδασκαλία |
Μαρία: Εννοείται ότι προτιμώ τον Ευκλείδη του Byrne! Δεν υπάρχει σύγκριση με τη διδασκαλία στον πίνακα! Μόνο και μόνο που δεν γράφουμε σύμβολα και σχέσεις στον πίνακα, είναι το πιο σημαντικό για μένα. […] Τα χρώματα που είδα στον διαδραστικό πίνακα με βοήθησαν να καταλάβω πολλά. | Συναισθήματα χαράς και αυτοπεποίθησης από τη χρήση του Ευκλείδη του Byrne Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne |
Ιωάννα: Ο Ευκλείδης του Byrne με τα χίλια! Χωρίς δεύτερη σκέψη! Τα χρώματα με τα οποία αποδείξαμε την πρόταση με βοήθησαν να την καταλάβω κατευθείαν, Δεν χρειάστηκε να αντιγράψω κάτι από τον πίνακα. Αυτό είναι το δύσκολο […] | Συναισθήματα χαράς και αυτοπεποίθησης από τη χρήση του Ευκλείδη του Byrne Κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων |
Πάνος: Προφανώς και προτιμώ τον Ευκλείδη του Byrne! Τα γράμματα [μεταβλητές] και οι εξισώσεις που χρησιμοποιούμε συνήθως στα Μαθηματικά με δυσκολεύουν αρκετά. Τώρα όμως κατάλαβα τι πρέπει να αποδείξω και πώς να το κάνω. […] Μου αρέσει επίσης να χρησιμοποιούμε τον διαδραστικό πίνακα στα Μαθηματικά. […] | Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων
Θετική επίδραση των ΤΠΕ στη διδασκαλία παιδιών με ΕΜΔ |
Επιλέξαμε χρώματα αντί για κωδικούς ή γράμματα, προκειμένου να συμβολίσουμε τις θεματικές ενότητες που προέκυψαν από τις συνεντεύξεις των παιδιών. Ο λόγος που το κάναμε αυτό ήταν για να είμαστε εγγύτερα στο “πνεύμα” του Ευκλείδη του Byrne, εφόσον η χρήση χρωμάτων είναι το βασικό χαρακτηριστικό για τον συμβολισμό πλευρών και γωνιών. Οι θεματικές ενότητες που προέκυψαν από τους κωδικούς είναι οι ακόλουθες:
Table 4. Θεματικές ενότητες
Κωδικοί | Χρώμα |
Η κατανόηση γεωμετρικών εννοιών με τη χρήση χρωμάτων μέσω του Ευκλείδη του Byrne | Κόκκινο |
Κατανόηση βασικών γεωμετρικών εννοιών | Μωβ |
Η χρήση του γραπτού λόγου προκαλεί δυσκολίες στα παιδιά με ΕΜΔ στην κατανόηση των εκφωνήσεων και στην κατανόηση των μαθηματικών συμβόλων | Πράσινο |
Αρνητικό συναίσθημα του παιδιού για τα Μαθηματικά με την παραδοσιακή διδασκαλία | Γαλάζιο |
Συναισθήματα χαράς και αυτοπεποίθησης από τη χρήση του Ευκλείδη του Byrne | Γκρι |
Θετική επίδραση των ΤΠΕ στη διδασκαλία παιδιών με ΕΜΔ | Καφέ |
Οι παραπάνω θεματικές ενότητες προέκυψαν από την ανάλυση των δεδομένων που αντλήθηκαν από τις συνεντεύξεις των μαθητών, και δείχνουν εν πολλοίς ότι η διδασκαλία σε παιδιά με ΕΜΔ που αξιοποιεί τον Ευκλείδη του Byrne, μπορεί να είναι πιο αποτελεσματική από την παραδοσιακή μέθοδο διδασκαλίας.
Πιο αναλυτικά, με σκοπό να απαντήσουμε στο ερευνητικό μας ερώτημα, αν δηλαδή ο Ευκλείδης του Byrne μπορεί να αποτελέσει μια αποτελεσματική μέθοδο διδασκαλίας, εφαρμόσαμε την εξής διδακτική διαδικασία: Μετά τις διακοπές των Χριστουγέννων, τον Ιανουάριο του 2023 (η αρχική, πεντάωρη διδακτική μας παρέμβαση πραγματοποιήθηκε την τελευταία εβδομάδα πριν το κλείσιμο των σχολείων, τον Δεκέμβριο του 2022) δώσαμε στους μαθητές μια άσκηση για το σπίτι η οποία ήταν παρόμοια με την απόδειξη της Πρότασης Ι.5, και τους ζητήσαμε να τη λύσουν με όποια μέθοδο επιθυμούν, είτε με την παραδοσιακή είτε με τον Ευκλείδη του Byrne. Επιπλέον, ανεβάσαμε στο e-class τον σύνδεσμο όπου υπάρχει ο Ευκλείδης του Byrne, με σκοπό τα παιδιά να μελετήσουν και να ξαναθυμηθούν την εν λόγω μέθοδο. Την επόμενη μέρα διαπιστώσαμε ότι όλα τα παιδιά είχαν λύσει την άσκηση με τη μέθοδο του Ευκλείδη του Byrne.
Στη συνέχεια ζητήσαμε από κάθε παιδί να λύσει την ίδια άσκηση με την κλασσική μέθοδο στον μαυροπίνακα. Για τον λόγο αυτό, ζητήσαμε από την καθηγήτρια μουσικής και την καθηγήτρια της γυμναστικής να απασχολήσουν τα υπόλοιπα παιδιά της τάξης όσο εμείς θα εξετάζαμε το κάθε παιδί ξεχωριστά από τα υπόλοιπα. Η εξέταση πραγματοποιήθηκε στην αίθουσα διδασκαλίας των παιδιών. Πιο συγκεκριμένα:
Πάνος: Όπως αναφέρθηκε στην προηγούμενη υποενότητα, ο Πάνος είναι ένας μαθητής με καλό μαθηματικό υπόβαθρο αλλά δυσκολεύεται να ανακαλέσει στη μνήμη του την προϋπάρχουσα γνώση. Όταν του ζητήθηκε να λύσει την άσκηση στον πίνακα με την παραδοσιακή μέθοδο διδασκαλίας, τα αποτελέσματα ήταν θετικά. Ειδικότερα, θυμήθηκε ότι πρέπει να προεκτείνουμε τις δύο πλευρές του τριγώνου και τις προέκτεινε με μαρκαδόρο διαφορετικού χρώματος, μας έδειξε τα τρίγωνα που πρέπει να συγκρίνουμε, και με το χέρι του μας έδειξε τα στοιχεία τους που είναι ίσα, ενώ και πάλι με το χέρι του μας υπέδειξε το επόμενο ζεύγος τριγώνων που πρέπει να συγκρίνουμε.
Όταν ο Πάνος συμμετείχε στην ομάδα που διδάχθηκε την πρόταση που αποδείξαμε στην διδακτική μας παρέμβαση με την κλασική μέθοδο διδασκαλίας, δυσκολευόταν να κατανοήσει τον λόγο για τον οποίο προεκτείναμε τις πλευρές του τριγώνου και να εντοπίσει τα ζεύγη των τριγώνων που έπρεπε να συγκρίνει. Όπως μας είπε: «Ο Ευκλείδης του Byrne με βοήθησε να θυμηθώ ποιες πλευρές πρέπει να προεκτείνω, να εντοπίζω τα τρίγωνα που πρέπει να συγκρίνω. Τα χρώματα που είχα δει στην απόδειξη που κάναμε με βοήθησαν να θυμηθώ και να καταλάβω τι πρέπει να κάνουμε». Ο Πάνος παρουσίασε πρόοδο, αφού ανακάλεσε πληροφορίες από την απόδειξη που είχε κάνει σπίτι του με τον Ευκλείδη του Byrne και τις χρησιμοποίησε στην παραδοσιακή μέθοδο διδασκαλίας.
Μαρία: Η Μαρία είναι μία μαθήτρια που έχει καλό μαθηματικό υπόβαθρο αλλά δυσκολεύεται να κάνει σχήματα στον μαυροπίνακα ή το τετράδιό της και να κατανοήσει γεωμετρικές σχέσεις. Όταν της ζητήθηκε να λύσει την άσκηση με βάση την παραδοσιακή μέθοδο διδασκαλίας, τα αποτελέσματα ήταν θετικά. Πιο συγκεκριμένα, κατάφερε να σχεδιάσει τις προεκτάσεις των γραμμών του τριγώνου με μαρκαδόρους διαφορετικού χρώματος και να εντοπίσει τα τρίγωνα που έπρεπε να συγκριθούν. Δυσκολεύτηκε λίγο στον εντοπισμό των στοιχείων των ίσων τριγώνων, αλλά τελικά τα εντόπισε, καθώς και στον εντοπισμό του επόμενου ζεύγους των ίσων τριγώνων.
Όταν η Μαρία ήταν στην ομάδα που διδάχθηκε την Πρόταση Ι.5 με την κλασσική μέθοδο διδασκαλίας, είχε δυσκολευτεί να κατανοήσει το σχήμα που κάναμε στον πίνακα. Επίσης, δεν μπορούσε να κατανοήσει τα ζεύγη των τριγώνων που έπρεπε να συγκριθούν. Η Μαρία μάς είπε: «Τα χρώματα που μας είχατε δείξει πριν τα Χριστούγεννα στην απόδειξη που κάναμε στον πίνακα αλλά και τα χρώματα που χρησιμοποίησα για να κάνω την άσκηση που είχαμε για το σπίτι, με βόηθησαν να καταλάβω ότι πρέπει να προεκτείνουμε τις πλευρές του τριγώνου. Δυσκολεύτηκα αλλά τελικά θυμήθηκα πώς να εντοπίσω τα ζεύγη των τριγώνων που πρέπει να συγκρίνω λόγω των χρωμάτων που χρησιμοποίησα στην άσκηση που είχαμε για το σπίτι».
Θάνος: Ο Θάνος είναι ένας μαθητής με χαμηλό μαθηματικό υπόβαθρο και δυσκολεύεται να κατανοήσει βασικές γεωμετρικές σχέσεις. Όταν του ζητήθηκε να λύσει την άσκηση που είχε για το σπίτι με την κλασσική μέθοδο διδασκαλίας, υπήρξε θετική ανταπόκριση ως προς κάποια σημεία. Πιο συγκεκριμένα, μπόρεσε να κατανοήσει ότι πρέπει να προεκτείνουμε τις πλευρές του τριγώνου και εντόπισε μόνος του το ζεύγος των προς σύγκριση τριγώνων. Ωστόσο, δεν μπόρεσε να βρει όλα τα απαιτούμενα στοιχεία των τριγώνων για να αποδείξει ότι είναι ίσα.
Όταν ο Θάνος συμμετείχε στην ομάδα που διδάχθηκε με την κλασική μεθοδολογία, δεν μπορούσε να καταλάβει γιατί προεκτείναμε τις πλευρές των τριγώνων. Επίσης, δεν είχε κατανοήσει γιατί συγκρίνουμε τα συγκεκριμένα ζεύγη τριγώνων και γιατί πρέπει να καταλήξουμε στο συμπέρασμα που μας ζητείται. Ο Θάνος δήλωσε: «Τα χρώματα που χρησιμοποιήσατε στον διαδραστικό πίνακα και οι εικόνες που είχε ο Ευκλείδης του Byrne με βοήθησαν να καταλάβω τα ίσα τρίγωνα. Τα χρώματα με βοήθησαν να κατανοήσω τις ίσες πλευρές των τριγώνων και πώς μπορώ να εντοπίζω τα τρίγωνα που πρέπει να συγκρίνω. Η μέθοδος που μας είχατε δείξει στον διαδραστικό πίνακα με βοήθησε να θυμηθώ ποιες πλευρές του τριγώνου πρέπει να προεκτείνω και ποια τρίγωνα πρέπει να συγκρίνω».
Ιωάννα: Η Ιωάννα είναι μια μαθήτρια με χαμηλό μαθηματικό υπόβαθρο, η οποία ενώ γνωρίζει τα βασικά γεωμετρικά σχήματα, δυσκολεύεται να τα σχεδιάσει στο τετράδιό της και στον πίνακα. Όταν της ζητήθηκε να λύσει την άσκηση με την παραδοσιακή μέθοδο διδασκαλίας, τα αποτελέσματα ήταν θετικά. Πιο συγκεκριμένα, μας ζήτησε και της δώσαμε χρωματιστούς μαρκαδόρους, και σχεδίασε μόνη της το τρίγωνο στον πίνακα. Επιπλέον, προέκτεινε τις πλευρές του τριγώνου μόνη της και κατάλαβε το αρχικό ζεύγος τριγώνων που έπρεπε να συγκρίνει.
Όταν η Ιωάννα συμμετείχε στην ομάδα που διδάχθηκε την απόδειξη της πρότασης με την παραδοσιακή μέθοδο διδασκαλίας, δυσκολεύτηκε να σχεδιάσει το τρίγωνο. Επίσης, δεν μπορούσε ούτε να εντοπίσει στον πίνακα τα ζεύγη των τριγώνων που έπρεπε να συγκριθούν, ούτε να προεκτείνει τις πλευρές του τριγώνου για να σχηματιστεί το άλλο ζεύγος των τριγώνων. Η Ιωάννα δήλωσε: «Όταν μας δείξατε την απόδειξη της πρότασης με τον Ευκλείδη του Byrne κατάλαβα αμέσως ποια τρίγωνα έπρεπε να συγκρίνω και πώς να τα σχεδιάσω. Τα χρώματα και τα σχήματα που υπάρχουν στον Ευκλείδη του Byrne με βοήθησαν να καταλάβω πώς να σχεδιάσω το τρίγωνο της άσκησης που μας βάλατε για το σπίτι και να θυμηθώ ποια τρίγωνα έπρεπε να συγκρίνω».
Γρηγόρης: Ο Γρηγόρης είναι ένας μαθητής με καλό μαθηματικό υπόβαθρο και μπορεί να κατανοήσει βασικές γεωμετρικές σχέσεις και να σχεδιάσει γεωμετρικά σχήματα. Όταν του ζητήθηκε να λύσει την άσκηση στον πίνακα με την παραδοσιακή μέθοδο διδασκαλίας, τα αποτελέσματα που προέκυψαν ήταν ενθαρρυντικά. Ειδικότερα, ο Γρηγόρης μπόρεσε να σχεδιάσει το τρίγωνο που έδινε η άσκηση (με μαρκαδόρους διαφορετικών χρωμάτων), να προεκτείνει τις πλευρές του και να εντοπίσει τα ζεύγη των τριγώνων που έπρεπε να συγκρίνει κάθε φορά. Τα στοιχεία των τριγώνων τα περιέγραφε βάσει των χρωμάτων και όχι με τη χρήση γεωμετρικών συμβόλων και σχέσεων.
Όταν ο Γρηγόρης συμμετείχε στην ομάδα που διδάχθηκε την πρόταση Ι.5 με την παραδοσιακή μέθοδο διδασκαλίας, δεν μπορούσε να καταλάβει γιατί πρέπει να προεκτείνουμε τις πλευρές του τριγώνου και δεν μπορούσε να εντοπίσει το δεύτερο ζεύγος των τριγώνων που έπρεπε να συγκρίνουμε. Ο Γρηγόρης μάς είπε: « Η απόδειξη που κάναμε με τη χρήση του Ευκλείδη του Byrne με βοήθησε να εντοπίσω κατευθείαν τα ζεύγη των τριγώνων που πρέπει να συγκρίνω, καθώς και τα στοιχεία των τριγώνων που είναι ίσα κάθε φορά. Γι’ αυτό σας ζήτησα και χρωματιστούς μαρκαδόρους για να μπορέσω να αποτυπώσω αυτά που σκέφτομαι με χρώματα. Τα γράμματα με δυσκολεύουν».
Κώστας: Ο Κώστας είναι ένας μαθητής με πολύ καλό μαθηματικό υπόβαθρο και μπορεί να απομνημονεύσει μαθηματικές και γεωμετρικές σχέσεις. Όταν έλυσε την άσκηση με την παραδοσιακή μέθοδο διδασκαλίας στον πίνακα, τα αποτελέσματα ήταν θετικά. Πιο συγκεκριμένα, μπόρεσε να σχεδιάσει το τρίγωνο (χρησιμοποιώντας και αυτός μαρκαδόρους διαφορετικών χρωμάτων), να εντοπίσει με σχετική ευκολία το πρώτος ζεύγος τριγώνων που έπρεπε να συγκρίνει, να προεκτείνει τις πλευρές του τριγώνου και να εντοπίσει το δεύτερο ζεύγος των τριγώνων που έπρεπε να συγκρίνει.
Όταν ο Κώστας ήταν στην ομάδα που διδάχθηκε την πρόταση Ι.5 με την κλασσική μέθοδο διδασκαλίας, δεν μπορούσε να καταλάβει τι έπρεπε να αποδείξουμε, αφού δυσκολευόταν να κατανοήσει τα γεωμετρικά σύμβολα που χρησιμοποιήσαμε για να παρουσιάσουμε την απόδειξη. Επιπλέον, δεν μπορούσε να καταλάβει γιατί προεκτείνουμε τις πλευρές του τριγώνου και αδυνατούσε να εντοπίσει το δεύτερο ζεύγος των τριγώνων που έπρεπε να συγκρίνουμε. Όπως ο ίδιος δήλωσε: «Όταν μας δείξατε στον διαδραστικό πίνακα την απόδειξη της πρότασης με τον Ευκλείδη του Byrne, μπόρεσα να καταλάβω τι μας ζητάει να αποδείξουμε η πρόταση και να διακρίνω αμέσως τα ζεύγη των τριγώνων που έπρεπε να συγκρίνω».
6. Συζητηση και συμπερασματςα
Η εισαγωγή των ΤΠΕ στον χώρο της Εκπαίδευσης, ήδη από τη δεκαετία του 1980 και τα ευρέως διαδεδομένα διαδραστικά εκπαιδευτικά λογισμικά (Cabri Geometry, The Geometer’s Sketchpad etc.), έχει επιφέρει σημαντικές αλλαγές στον τρόπο διδασκαλίας και μάθησης των Μαθηματικών. Τα τελευταία τρία χρόνια ωστόσο, ιδιαίτερα στην Ελλάδα, λόγω της πανδημίας Covid-19 και της επιβεβλημένης, εκ των πραγμάτων, εξ αποστάσεως εκπαίδευσης, η ανάγκη για επιμόρφωση των εκπαιδευτικών επάνω στα νέα ψηφιακά εργαλεία (platforms, courses management systems, collaboration tools etc.) έγινε επιτακτική, ενώ παράλληλα νέες διδακτικές τεχνικές ήρθαν στο προσκήνιο (Rizos & Gkrekas, 2022; Rizos et al. 2023). Επιπλέον, με απόφαση του Ελληνικού Υπουργείου Παιδείας (Φ.478.6/104/66585/Α2/8-06-2021), όλες οι σχολικές μονάδες της Πρωτοβάθμιας και Δευτεροβάθμιας εκπαίδευσης προμηθεύτηκαν ή θα προμηθευτούν διαδραστικούς πίνακες. Υπ’ αυτή την έννοια ο Ευκλείδης του Byrne αποτελεί ένα σύγχρονο οπτικό βοήθημα, το οποίο φαίνεται πως προσελκύει το ενδιαφέρον όλο και περισσότερων δασκάλων και ερευνητών σε όλο τον κόσμο. Ωστόσο, η έρευνα για την αξιοποίησή του σε παιδιά με ΕΜΔ είναι πολύ περιορισμένη τόσο σε ελληνικό, όσο και σε διεθνές επίπεδο. Προς την κάλυψη αυτού του κενού φιλοδοξεί να συμβάλει η παρούσα εργασία.
Στο άρθρο αυτό εξετάζουμε την επίδραση του οπτικού εργαλείου “Ο Ευκλείδης του Byrne” στη διδασκαλία της Ευκλείδειας Γεωμετρίας σε παιδιά με ΕΜΔ σε ένα Ενιαίο Ειδικό Επαγγελματικό Γυμνάσιο στην Ελλάδα. Η έρευνά μας αποκάλυψε τα ακόλουθα πλεονεκτήματα που έχει η χρήση του Ευκλείδη του Byrne στο παραπάνω πλαίσιο:
- Αφομοίωση των βασικών γεωμετρικών εννοιών
- Αύξηση της μαθησιακής εμπλοκής στην επίλυση γεωμετρικών προβλημάτων
- Κατανόηση των βασικών σημείων μιας γεωμετρικής απόδειξης
- Ενεργός εμπλοκή όλων των μαθητών της τάξης στην επίλυση γεωμετρικών προβλημάτων με τη χρήση χρωμάτων
- Καλλιέργεια θετικής στάσης απέναντι στο μάθημα της Γεωμετρίας και γενικότερα των Μαθηματικών.
Ένα από τα ευρήματα που προέκυψαν από τη διδακτική μας παρέμβαση είναι ότι η χρήση του Ευκλείδη του Byrne βελτιώνει τις μαθηματικές ικανότητες των μαθητών, την οπτική τους αντίληψη και τις μεταγνωστικές τους δεξιότητες, όπως είναι η λύση προβλήματος. Σε αυτό συμφωνούν και οι Chatzivasileiou & Driga (2022). Επιπλέον, υπήρξε ενεργός συμμετοχή όλων των παιδιών στο μάθημα της Γεωμετρίας όταν χρησιμοποιήθηκε για την απόδειξη της πρότασης Ι.5 ο Ευκλείδης του Byrne, γεγονός με το οποίο η έρευνα συγκλίνει (see Toney et al., 2013). Ακόμη, οι μαθητές μπόρεσαν να συγκρατήσουν στη μνήμη τους πολλά στοιχεία από την απόδειξη της πρότασης Ι.5 με τα σχήματα και τα χρώματα που υπήρχαν στον Ευκλείδη του Byrne, κάτι που επιβεβαιώνεται και από την έρευνα του Pedeferri (2020).
Ωστόσο, υπάρχουν και περιορισμοί που προέκυψαν κατά τη διάρκεια της ερευνητικής διαδικασίας. Οι κυριότεροι είναι οι ακόλουθοι:
Ο χρόνος που χρειάστηκαν τα παιδιά για να επιλύσουν την άσκηση για το σπίτι που ήταν αναρτημένη στην πλατφόρμα e-class
Μαθησιακά κενά που είχαν τα παιδιά σε βασικές γεωμετρικές έννοιες.
Οι μαθητές που φοιτούν στα σχολεία στην Ελλάδα έχουν καθημερινά πολλές ώρες διαβάσματος στο σπίτι, με αποτέλεσμα να δυσκολεύονται να ανταπεξέλθουν στις υποχρεώσεις τους όταν σε ένα μάθημα έχουν επιπλέον φόρτο εργασίας. Χαρακτηριστικά, ο Γρηγόρης μάς είπε: «Για να προλάβω να κάνω την εργασία που μου βάλατε, μείωσα τον χρόνο που θα διέθετα για να διαβάσω τα υπόλοιπα μαθήματα […] Θα προτιμούσα ωστόσο να έχουμε μια παρόμοια εργασία και στην Άλγεβρα». Επιπλέον, τα παιδιά παρουσίαζαν ελλείμματα σε βασικές έννοιες της Γεωμετρίας (π.χ. διαχωρισμός πλευράς από γωνία), αφού πριν τη χρήση του διαδραστικού πίνακα, η διδασκαλία της Γεωμετρίας γινόταν αποκλειστικά και μόνο σε μαυροπίνακα. Η αξιοποίηση του Ευκλείδη του Byrne στον διαδραστικό πίνακα κάλυψε μέρος των κενών που είχαν οι μαθητές.
Όσον αφορά τα επιτεύγματα των παιδιών μετά τη διδασκαλία με τη χρήση του Ευκλείδη του Byrne, αυτά φαίνονται από:
Την επίλυση της άσκησης στην πλατφόρμα e-class, με την κατ’ επιλογή χρήση του Ευκλείδη του Byrne έναντι του παραδοσιακού τρόπου που χρησιμοποιούνταν στην τάξη μέχρι τότε
Τη χρήση τεχνικών από τον Ευκλείδη του Byrne στην επίλυση της ίδιας άσκησης στον μαυροπίνακα της τάξης
Τη συζήτηση που πραγματοποιήθηκε στο πλαίσιο των ερευνητικών συνεντεύξεων με τον κάθε μαθητή.
Από την έρευνα που διεξαγάγαμε προκύπτει ότι το ερευνητικό μας ερώτημα έχει θετική απάντηση. Δηλαδή, η διδασκαλία βασικών εννοιών και διαδικασιών σε μαθητές Γυμνασίου με ΕΜΔ με τη χρήση της ιστοσελίδας “Ο Ευκλείδης του Byrne”, έχει καλύτερα μαθησιακά αποτελέσματα σε σχέση με την παραδοσιακή διδασκαλία. Πιο συγκεκριμένα, μετά το πέρας της διδακτικής μας παρέμβασης, όλοι οι συμμετέχοντες μαθητές ήταν σε θέση να αντιληφθούν τα βασικά σημεία της απόδειξης που τους παρουσιάσαμε, να κατανοήσουν τις βασικές γεωμετρικές έννοιες που απαιτούνταν για την απόδειξη της πρότασης Ι.5 και να εντοπίσουν στον μαυροπίνακα μόνοι τους τα ζεύγη και τα στοιχεία των τριγώνων που έπρεπε να συγκρίνουν. Επιπλέον, οι μαθητές καλλιέργησαν θετική στάση για το μάθημα της Γεωμετρίας και των Μαθηματικών γενικότερα, κάτι το οποίο δεν ίσχυε όταν οι βασικές γεωμετρικές έννοιες και ασκήσεις διδάσκονταν με την παραδοσιακή μέθοδο διδασκαλίας στον μαυροπίνακα.
Βάσει των αποτελεσμάτων της διδακτικής παρέμβασης που υλοποιήσαμε, προκύπτει ότι η διδασκαλία της Ευκλείδειας Γεωμετρίας σε παιδιά με ΕΜΔ με τη χρήση του Ευκλείδη του Byrne προωθεί την ενεργό συμμετοχή στην επίλυση γεωμετρικών ασκήσεων. Επιπλέον, ο Ευκλείδης του Byrne μπορεί να αποτελέσει ένα χρήσιμο διδακτικό εργαλείο για την παρουσίαση από τους εκπαιδευτικούς βασικών γεωμετρικών εννοιών και διαδικασιών της Ευκλείδειας Γεωμετρίας τόσο σε Ειδικά Επαγγελματικά Γυμνάσια όσο και σε Γενικά Γυμνάσια, αφού τα χρώματα και οι εικόνες που περιέχει συμβάλλουν στην καλύτερη κατανόηση των γεωμετρικών εννοιών και διαδικασιών από τα παιδιά. Στα Γενικά Γυμνάσια υπάρχουν παιδιά με δυσλεξία που φοιτούν σε Τμήματα Ένταξης, τα οποία αντιμετωπίζουν δυσκολίες στην κατανόηση του γραπτού λόγου. Ενδεχομένως η αξιοποίηση του Ευκλείδη του Byrne στη διδασκαλία της Γεωμετρίας σε παιδιά με δυσλεξία που φοιτούν σε Τμήματα Ένταξης των Γενικών Σχολείων, μπορεί να επιφέρει θετικά μαθησιακά αποτελέσματα. Μία μελλοντική έρευνα θα μπορούσε να επιβεβαιώσει ή να απορρίψει αυτή την εικασία.
Βιβλιογραφία
Abreu, R. L., Townsend, D., Mitchell, Y., Ward, J., Audette, L., & Gonzalez, K. A. (2022). LGBTQ Qualitative and Mixed Methods Research in Counseling Psychology: A Content Analysis. The Counseling Psychologist, 50(5), 708-737. https://doi.org/10.1177/00110000221092481
Barnes, M. A., Clemens, N. H., Fall, A.-M., Roberts, G., Klein, A., Starkey, P., McCandliss, B., Zucker, T., & Flynn, K. (2020). Cognitive predictors of difficulties in math and reading in pre-kindergarten children at high risk for learning disabilities. Journal of Educational Psychology, 112(4), 685-700. https://doi.org/10.1037/edu0000404
Bolondi, G., & Luigini, A. (2018). Byrne’s Euclidean Geometry Revisited with Geogebra. ICGG 2018: Proceedings of the 18th International Conference on Geometry and Graphics; 40th Anniversary, Milan, Italy, August 3-7, 2018, 809, 1468-1473. https://doi.org/10.1007/978-3-319-95588-9_129
Cass, M., Cates, D., Smith, M., & Jackson, C. (2003). Effects of Manipulative Instruction on Solving Area and Perimeter Problems by Students with Learning Disabilities. Learning Disabilities Research & Practice, 18, 112-120. https://doi.org/10.1111/1540-5826.00067
Chatzivasileiou, P., & Drigas, A. (2022). ICTs for the Cognitive and Metacognitive abilities of the students with Specific Learning Disorder in Mathematics. Technium Social Sciences Journal, 31(1), 256–279. https://doi.org/10.47577/tssj.v31i1.6424
Cirafici, A. (2018). Ad Oculos. Images, Imagination and Abstract Thinking. Proceedings of the International and Interdisciplinary Conference IMMAGINI? Brixen, Italy, 27-28 November 2017. MDPI. Retrieved from http://dx.doi.org/10.3390/proceedings1090945
Clements, D. H., & Battista, M. T. (1992). Geometry and spatial reasoning. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 420-464). New York: Macmillan.
Grigorenko, E. L., Compton, D. L., Fuchs, L. S., Wagner, R. K., Willcutt, E. G., & Fletcher, J. M. (2020). Understanding, educating, and supporting children with specific learning disabilities: 50 years of science and practice. American Psychologist, 75(1), 37-51. https://doi.org/10.1037/amp0000452
Grobecker, B., & De Lisi, R. (2000). An Investigation of Spatial-Geometrical Understanding in Students with Learning Disabilities. Learning Disability Quarterly, 23(1), 7-22. https://doi.org/10.2307/1511096
Hawes, S. M., & Kolpas, S. (2015). Oliver Byrne: The Matisse of Mathematics. Mathematical Association of America. https://doi.org/10.4169/convergence20150803
Jitendra, A. K., Lein, A. E., Im, S., Alghamdi, A. A., Hefte, S. B., & Mouanoutoua, J. (2018). Mathematical Interventions for Secondary Students with Learning Disabilities and Mathematics Difficulties: A Meta-Analysis. Exceptional Children, 84(2), 177-196. https://doi.org/10.1177/0014402917737467
Kellems, R. O., Eichelberger, C., Cacciatore, G., Jensen, M., Frazier, B., Simons, K., & Zaru, M. (2020). Using Video-Based Instruction via Augmented Reality to Teach Mathematics to Middle School Students With Learning Disabilities. Journal of Learning Disabilities, 53(4), 277-291. https://doi.org/10.1177/0022219420906452
Mammarella, I. C., Giofrè, D., Ferrara, R. & Cornoldi, C. (2013). Intuitive geometry and visuospatial working memory in children showing symptoms of nonverbal learning disabilities. Child Neuropsychology, 19(3), 235-249. https://doi.org/10.1080/09297049.2011.640931
Marita, S., & Hord, C. (2017). Review of Mathematics Interventions for Secondary Students With Learning Disabilities. Learning Disability Quarterly, 40(1), 29-40. https://doi.org/10.1177/0731948716657495
Pedeferri, A. (2020). Visual Representations of Euclidean Geometry: Diagrammatic Reasoning in Oliver Byrne’s Work. In: B. Sriraman (Ed.) Handbook of the History and Philosophy of Mathematical Practice. Springer, Cham. https://doi.org/10.1007/978-3-030-19071-2_25-1
Rizos, I., & Gkrekas, N. (2022). Teaching and learning sciences within the COVID-19 pandemic era in a Greek university department. Porto Journal of Engineering, 8(1), 73-83. https://doi.org/10.24840/2183-6493_008.001_0008
Rizos, I., Kolokotronis, G., & Papanikolaou, A. M. (2023). Investigating the effectiveness of Flipped Classroom model in a Mathematics Education course in Greece. Journal of Mathematics and Science Teacher, 3(1), em021. https://doi.org/10.29333/mathsciteacher/12608
Soares, N., Evans, T., & Patel, D. (2017). Specific learning disability in mathematics: a comprehensive review. Translational Pediatrics, 7(1), 48-62. doi:10.21037/tp.2017.08.03
Toney, A. F., Slaten, K. M., Peters, E. F., & Hauk, S. (2013). Color Work to Enhance Proof-Writing in Geometry. Journal of the California Mathematics Project, 6(1), 9-19.
Willcutt, E. G., McGrath, L. M., Pennington, B. F., Keenan, J. M., DeFries, J. C., Olson, R. K., & Wadsworth, S. J. (2019). Understanding Comorbidity Between Specific Learning Disabilities. ln L. S. Fuchs & D. L. Compton (Eds), Models for Innovation: Advancing Approaches to Higher-Risk and Higher-Impact Learning Disabilities Science. New Directions for Child and Adolescent Development, 165, 91-109. https://doi.org/10.1002/cad.20291
Όλες οι σημαντικές και έκτακτες ειδήσεις σήμερα
Πώς τα χρήματά σας «φεύγουν» αθόρυβα από τον τραπεζικό σας λογαριασμό
Σπίτι με 50 ευρώ το μήνα για δημόσιους υπαλλήλους: Το νέο πρόγραμμα που αλλάζει τα δεδομένα





