Alfavita Newsroom Θα μπορούσε ένας αστροναύτης εκτελώντας ένα άλμα από το διαστημόπλοιό του να βρεθεί πάνω σ’ έναν κομήτη;
Όπως ίσως θα έχετε ήδη πληροφορηθεί το διαστημικό σκάφος Rosetta προσεγγίζει τον κομήτη 67P/Churyumov-Gerasimenko και σε λίγες ημέρες θα αρχίσει να κάνει περίπλοκους ελιγμούς γύρω από τον κομήτη για να χαρτογραφήσει την επιφάνειά του, ώστε οι υπεύθυνοι της αποστολής να αποφασίσουν για το κατάλληλο σημείο στο οποίο θα προσεδαφιστεί το ειδικό όχημα Philae.
Βίντεο: Η τροχιά της Rosetta γύρω από τον κομήτη 67Ρ
Η προσεδάφιση είναι προγραμματισμένη για το Νοέμβριο, όταν το Philae θα ρίξει άγκυρες (ακριβώς όπως ακούγεται) ώστε να αγκιστρωθεί στον κομήτη 67Ρ! (διαβάστε περισσότεραΕΔΩ)
Ο Rhett Allain από το πανεπιστήμιο της Louisiana, που συνεργάζεται με την ερευνητική ομάδα της διαστημικής αποστολής Rosetta, θέτει και απαντά στο ερώτημα:
«Θα μπορούσε ένας αστροναύτης εκτελώντας ένα άλμα από το διαστημόπλοιό του να βρεθεί πάνω στον κομήτη;»
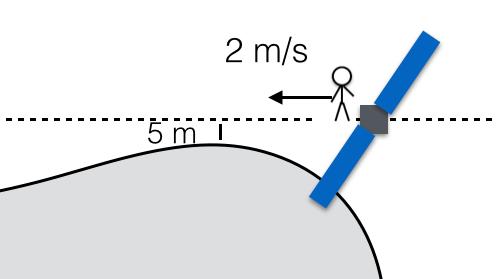
Η απάντηση μπορεί να δοθεί με απλή φυσική. Ας υποθέσουμε ότι στο διαστημικό σκάφος Rosetta βρισκόταν ένας αστροναύτης έτοιμος για όλα, και το σκάφος πλησίαζε τον κομήτη σε απόσταση 5 μέτρων με μια ταχύτητα 2 m/s – σε σχέση με τον κομήτη:
Ας κάνουμε μερικές ακόμα εύλογες υποθέσεις:
• Ο κόμητης 67Ρ έχει μάζα 3,14•1012 kg και υποθέτουμε ότι είναι σφαιρικός με ακτίνα 2 km – μια υπόθεση που δεν βλάπτει τη γενικότητα.
• Κατά τη στιγμή του άλματος το διαστημικό σκάφος Rosetta κινείται σχεδόν παράλληλα με τον κομήτη
• Η Rosetta έχει μάζα περίπου 1580 kg
• O αστροναύτης μαζί με τη στολή του έχει μάζα 80 kg
• Η βαρυτική δύναμη από τον Ήλιο είναι σχεδόν σταθερή στη θέση αυτή (η πιο σίγουρη υπόθεση)
• Η επιτάχυνση του κομήτη εξαιτίας της τροχιακής του κίνησης είναι επίσης μικρή. Αυτό σημαίνει ότι στο σύστημα αναφοράς του κομήτη μπορούμε να αγνοήσουμε τις αδρανειακές δυνάμεις, φυγόκεντρο δύναμη και Coriolis.
Θεωρήσαμε ότι το σκάφος κινείται με ταχύτητα 2 m/s σε σχέση με τον κομήτη στον οποίο πρέπει να πηδήξει με ασφάλεια ο αστροναύτης, δηλαδή να προσγειωθεί σ’ αυτόν με μηδενική ταχύτητα.
Ένα επιτόπιο άλμα στην επιφάνεια της Γης
Έστω ότι στην επιφάνεια της Γης ο αστροναύτης μπορεί να κάνει ένα επιτόπιο άλμα ύψους 20 cm (μετατόπιση του κέντρου μάζας του)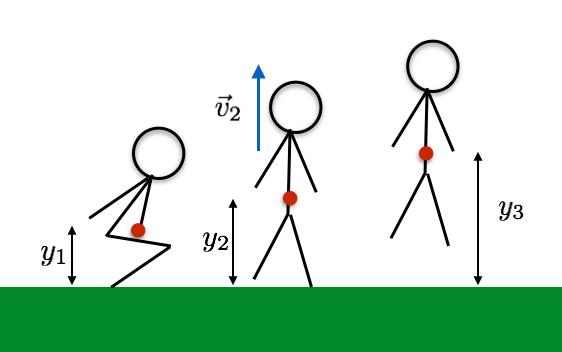
Kατά τη διάρκεια αυτής της διαδικασίας (σύμφωνα με το παραπάνω σχήμα) ο αστροναύτης μετακινεί το κέντρο μάζας του από τη θέση y1 στη θέση y2 , όπου εκτοξεύεται προς τα πάνω. Στη θέση y2 ο αστροναύτης παύει να έχει επαφή με το έδαφος, αλλά έχει αποκτήσει μια ταχύτητα με την οποία εκτοξεύεται προς τα πάνω.
Αυτό που χρειαζόμαστε είναι το έργο που κατανάλωσε ο αστροναύτης για να επιτύχει το άλμα του.
Μια λογική εκτίμηση των τριών θέσεων του κέντρου μάζας, σύμφωνα με τον Rhett Allain, είναι: y1=75 cm, y2=103 cm και y3=123 cm.
Δεδομένου ότι στην αρχική και την τελική θέση η ταχύτητα του αστροναύτη είναι μηδέν, το έργο που καταναλώθηκε για την μετακίνηση αυτή (Δh = 0,48 m), ισούται με την μεταβολή της βαρυτικής δυναμικής ενέργειας:
W=m g Δh = 80•9,8•0,48 = 376,3 joules
Μπορούμε εύκολα αν βρούμε ότι η ταχύτητα με την οποία αφήνει το έδαφος ο αστροναύτης, ώστε να φτάσει σε ύψος 20 cm, είναι περίπου 2 m/s.
Και τώρα ας υποθέσουμε πως όταν ο αστροναύτης πηδάει από τη Rosetta προς τον κομήτη, καταναλώνει την ίδια ποσότητα ενέργειας με το επιτόπιο άλμα στη Γη.
Πηδώντας από ένα διαστημικό σκάφος
Αν ένας αστροναύτης μπορεί να κάνει ένα επιτόπιο άλμα στη Γη με αρχική ταχύτητα 2m/s, δεν θα μπορούσε να πηδήξει από ένα διαστημικό σκάφος με την ίδια ταχύτητα;
Εδώ υπάρχει μια σημαντική διαφορά – το διαστημικό σκάφος, εξαιτίας της αρχής διατήρησης της ορμής, θα μετακινηθεί προς την αντίθετη κατεύθυνση καθώς ο αστροναύτης θα εκτελεί το άλμα του:
Eφαρμόζοντας την αρχή διατήρησης της ορμής για το σύστημα αστροναύτης – Rosetta έχουμε
ενώ από την αρχή διατήρησης της ενέργειας προκύπτει:
Λύνοντας το σύστημα των δυο εξισώσεων οι ταχύτητες του αστροναύτη και της Rosetta θα υπολογίζονται από τις εξισώσεις:
Aντικαθιστώντας τις τιμές των μεγεθών στις παραπάνω εξισώσεις προκύπτει ότι ο αστροναύτης αποκτά ταχύτητα 3 m/s, ενώ η ταχύτητα ανάκρουσης της Rosetta θα είναι 0,15 m/s.
Μπορεί τελικά ο αστροναύτης να κάνει άλμα προς τον κομήτη;
Ναι. Καθώς το διαστημικό σκάφος Rosetta κινείται με μια ταχύτητα περίπου 2 m/s ως προς τον κομήτη ο αστροναύτης πηδάει από το σκάφος. Δεδομένου ότι αποδείξαμε πως μπορεί να πηδήξει από το σκάφος με ταχύτητα πάνω από 2 m/s, τότε προφανώς θα μπορούσε να εκτελέσει το άλμα του με τέτοια κατεύθυνση, έτσι ώστε μόλις εγκαταλείψει το σκάφος, να είναι σχεδόν ακίνητος ως προς τον κομήτη.
Τότε θα μπορούσε ο αστροναύτης να «πέσει ελεύθερα» προς τον κομήτη;
Χρησιμοποιώντας το νόμο της παγκόσμιας έλξης
προκύπτει ότι η βαρυτική δύναμη που αισθάνεται ο αστροναύτης εξαιτίας του κομήτη είναι 0,0042 Ν και η επιτάχυνση κατά την ελεύθερη πτώση του προς τον κομήτη θα είναι 5,24•10-5m/s2.
Πόσος χρόνος θα απαιτηθεί για να φτάσει ο αστροναύτης στην επιφάνεια του κομήτη από ύψος 5 μέτρων;
Μπορεί να είναι μια ελεύθερη πτώση μεγάλης διάρκειας 437 δευτερολέπτων (περίπου 7,3 λεπτά), αλλά είναι εφικτή.
Συνεπώς η απάντηση στο αρχικό ερώτημα είναι καταφατική. Ένας αστροναύτης θα μπορούσε να πηδήξει από το διαστημικό του σκάφος και να προσγειωθεί σε έναν κομήτη.
Δεν μένει παρά να το πραγματοποιήσουμε.
Διαβάστε περισσότερες λεπτομέρειες ΕΔΩ: blogs.esa.int - physicsgg.me/
Όλες οι σημαντικές και έκτακτες ειδήσεις σήμερα
Είσαι άνεργος στο κέντρο της Αθήνας; ΠΑΡΕ ΤΩΡΑ έκτακτο επίδομα 1000 ευρώ
ΕΛΜΕΠΑ: Το κορυφαίο πρόγραμμα Ειδικής Αγωγής στην Ελλάδα για διπλή μοριοδότηση
Το 1ο στην Ελλάδα Πρόγραμμα επιμόρφωσης Τεχνητής Νοημοσύνης για εκπαιδευτικούς με Πιστοποιητικό
ΑΣΕΠ: Η πιο Εύκολη Πιστοποίηση Αγγλικών για μόρια σε 2 ημέρες (δίνεις από το σπίτι σου με 95 ευρώ)
Παν.Πατρών: Μοριοδοτούμενο σεμινάριο ΕΙΔΙΚΗ ΑΓΩΓΗΣ με 65Є εγγραφή - έως 24/12
ΕΥΚΟΛΕΣ πιστοποιήσεις ΙΣΠΑΝΙΚΩΝ - ΙΤΑΛΙΚΩΝ - ΓΑΛΛΙΚΩΝ - ΓΕΡΜΑΝΙΚΩΝ για ΑΣΕΠ - Πάρτε τις ΑΜΕΣΑ
